Неопределенность или непредсказуемость момента смерти, заболевания, аварии является основным источником случайности при страховании, что позволяет использовать случайные события, величины, процессы при математическом анализе различных аспектов страхования жизни, здоровья, автомобиля и т.п. Очевидно, что относительно момента смерти конкретного человека, как правило, трудно сказать что-либо определенное. Однако, если рассматривается достаточно большая однородная группа людей, то для нее уже будут справедливы закономерности, присущие массовым случайным явлениям, например, устойчивость частот, сходимость к нормальному или пуассоновскому законам распределения и так далее. Поэтому, привлекая терминологию теории вероятностей, можно говорить о продолжительности жизни как о случайной величине, которая принимает только положительные значения.
Одной из основных характеристик в актуарной математике является функция выживания 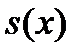 , означающая долю лиц из некоторой условной совокупности, доживающих до возраста x.
, означающая долю лиц из некоторой условной совокупности, доживающих до возраста x.
Конечно, 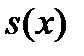 - не что иное, как вероятность для наугад выбранного лица из данной совокупности родившихся дожить до возраста x.
- не что иное, как вероятность для наугад выбранного лица из данной совокупности родившихся дожить до возраста x.
Продолжительность жизни T для произвольно выбранного лица естьслучайная величина. Факт достижения им возраста x записывается в виде неравенства 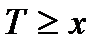 , а вероятность
, а вероятность 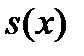 - в виде
- в виде
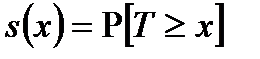
Дополнение до 1, то есть функция
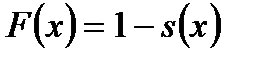
называется функцией распределенияпродолжительности жизни. Вероятностный смысл ее описывается равенством
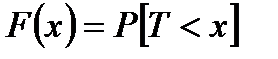
то есть это вероятность того, что данное родившееся лицо не доживет до возраста x.
В страховании часто используют условные случайные величины и соответствующие распределения. Пусть 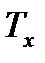 – остаточное время жизни для произвольного выбранного лица возраста x, то число
– остаточное время жизни для произвольного выбранного лица возраста x, то число

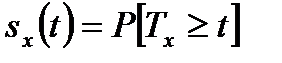
будет условной вероятностью
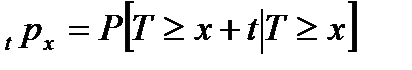
дожития до возраста x+t лет для лица, имеющего возраст x лет. Используя элементарные тождества теории вероятностей, можно показать, что
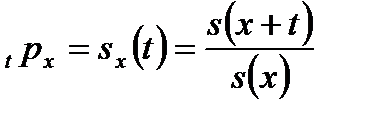 .
.
Соответственно условная вероятность смерти лица возраста x в промежутке 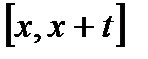 есть
есть
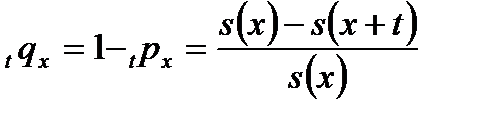 .
.
Тогда доля лиц, умирающих в единицу времени в этом промежутке, есть
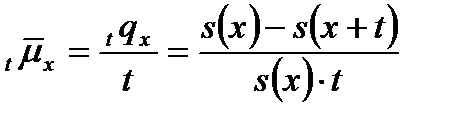
Величина 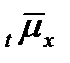 характеризуетинтенсивность смерти лиц, достигших возраста x. Переходя к пределу, получим:
характеризуетинтенсивность смерти лиц, достигших возраста x. Переходя к пределу, получим:
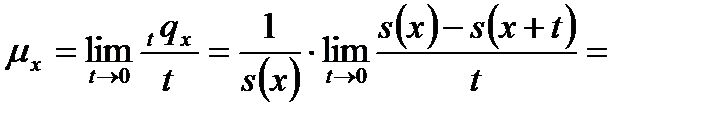
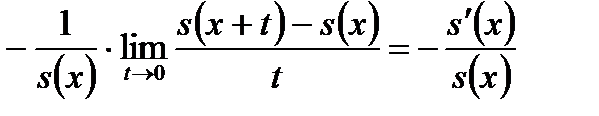 (12)
(12)
предел
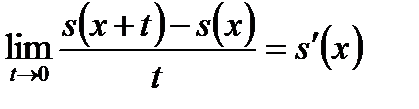
называют производной функции 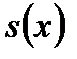 в точке x.
в точке x.
Величина 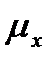 называется интенсивностью (силой) смертности в возрасте x. Это важная характеристика процесса вымирания данной группы населения.
называется интенсивностью (силой) смертности в возрасте x. Это важная характеристика процесса вымирания данной группы населения.
Величины 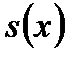 и
и 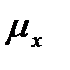 , являются взаимопределяемыми:
, являются взаимопределяемыми:
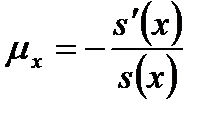 .
.
С другой стороны это равенство означает, что
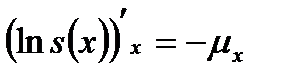 или
или 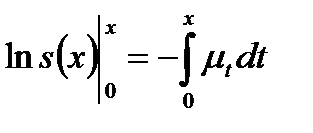
и, наконец,
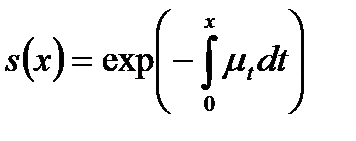 , т.к.
, т.к. 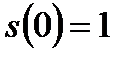 .
.
Так же выводим уравнение для условной функции выживания
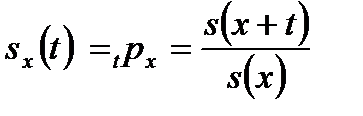 .
.
Из данного равенства следует:
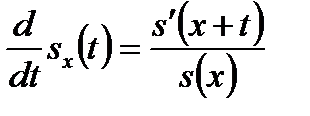 ,
,
а так как на основании (12)
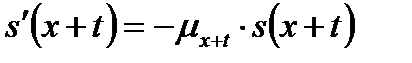 , то
, то
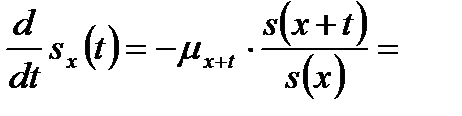
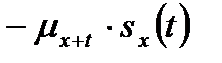 .
.
Отсюда получаем, что
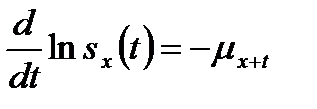 или
или 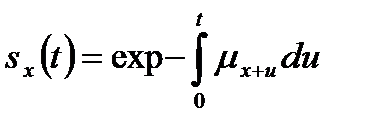 .
.
Поскольку
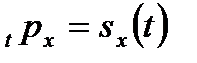 и
и 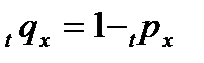 ,
,
то
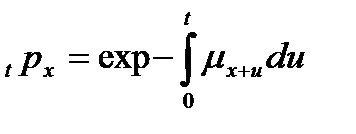 и
и 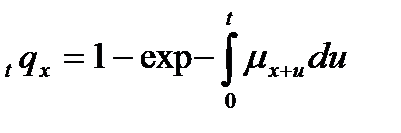
Вышеприведенные формулы относятся к вероятностнымфункциям дожития 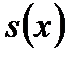 и
и 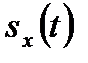 .
.
Часто вместо них рассматривается функция 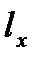
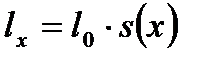 и
и 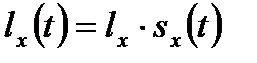 ,
,
относящаяся к некоторым исходным совокупностям 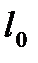 .
.
 2015-08-12
2015-08-12 2805
2805
