Элементы финансовой математики, применяемые в страховой деятельности

В актуарных расчетах активно используются финансовые инструменты для оптимизации финансовых потоков, стабильности финансовых операций и предполагаемой прибыли страховой компании.

Предположим, что в момент времени 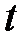дается в долг сумма . Через некоторое время 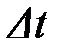рассчитывается на определенный доход 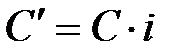от инвестирования принадлежащего капитала . Сумма 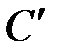- есть награда за то, что средства использовались другим человеком. Обычно ее измеряют в относительных единицах; величина 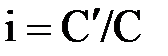называется эффективной процентной ставкой за рассматриваемый промежуток времени .

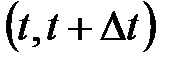Если предполагать, что сумма может инвестироваться на два последовательных промежутка времени. Пусть 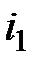– эффективная процентная ставка на первом промежутке, 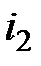–на втором. Имеются две схемы исчисления дохода 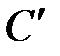на объединенном интервале:

- принцип простых процентов полагает, что проценты начисляют только на основной капитал. Поэтому 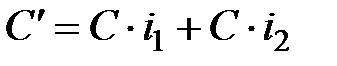. Соответственно, итоговая процентная ставка .

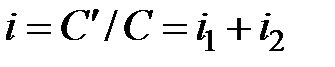- принцип сложных процентов полагает, что проценты начисляются не только на основной капитал, но и на уже полученные проценты. Поэтому в конце второго интервала времени основной капитал вырастет до величины 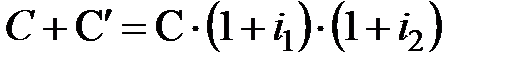.Соответственно, итоговая процентная ставка 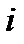определяется из условия 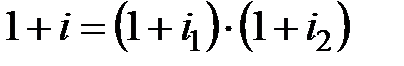, т.е. .

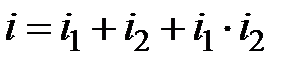- принцип сложных процентов обозначает, что вкладчик может свободно распоряжаться своими финансами. Поэтому в актуарной математике принято применять принцип сложных процентов при определении дохода от вложенных средств.

- процентные ставки, применяемые в большинстве расчетов в актуарной математике, определяются, исходя из консервативных оценок доходности истинных будущих вложений страховщика. Они намного ниже реальных процентных ставок, предлагаемых рынком для всяческих видов инвестиционных проектов. Их смысл заключается в том, чтобы как-нибудь учитывать рост денег, которые внесены в качестве платы за страховое покрытие. Поэтому их называют техническими процентными ставками. На самом деле страховая компания зарабатывает гораздо существеннее проценты; более того, это один из самых значимых источник дохода страховщика.

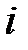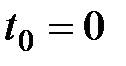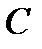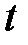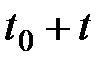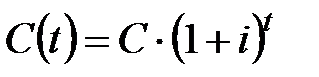Возьмем некоторый промежуток времени в качестве единичного и будем полагать, что процентная ставка за этот промежуток равна . Допустим, что в момент сумма инвестируется на единиц времени. По принципу сложных процентов в момент времени капитал превратится в сумму . Величина 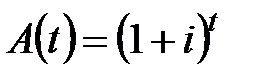называется коэффициентом накопления за время [8].

Интенсивность процентов 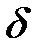– это мгновенная относительная скорость накопления средств

.

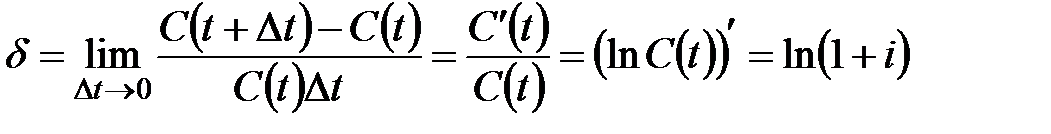Поскольку 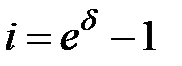, то коэффициент накопления за время можно представить в виде

.

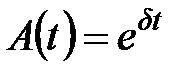Интенсивность процентов подходит для использования изучения накоплений в случае меняющихся процентных ставок. В этом случае 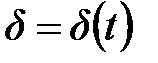и

.

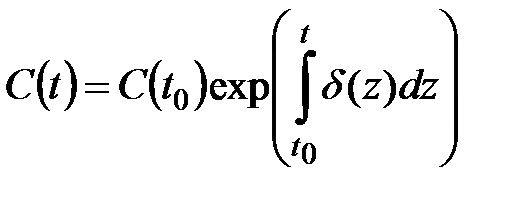Рассмотрим промежуток времени длиной 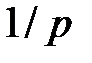. Если в качестве единицы измерения принят один год, то наиболее часто встречаются случаи: 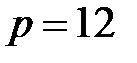(рассматриваемый промежуток времени равен одному месяцу); 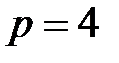(квартал); 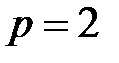(полугодие).

Эффективная процентная ставка 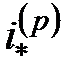за этот промежуток времени равна

.

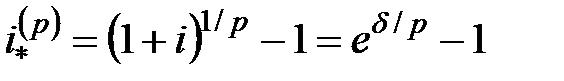Однако в финансовой математике принято характеризовать доходность вложения средств на промежутке 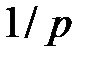не эффективной (т.е. реальной) процентной ставкой 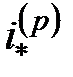, а так называемой номинальной процентной ставкой

.

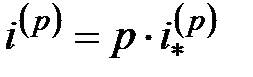Иногда величину 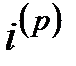называют номинальной процентной ставкой выплачиваемой (начисляемой) с частотой 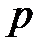[5].

Приведенная ценность

Величину 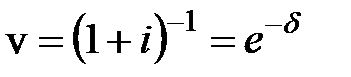называют коэффициентом дисконтирования (учета). С ее помощью формулу для приведенной стоимости можно записать в виде

.

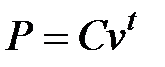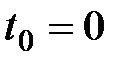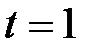Предположим, что в момент мы даем взаймы сумму . Тогда в момент нам должны вернуть сумму 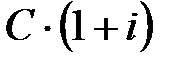, которая формируется из двух частей: возврата основного капитала и процентов на капитал .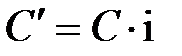

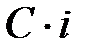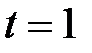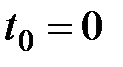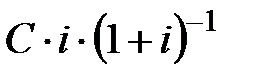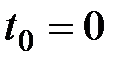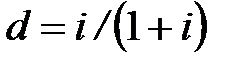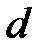Если сумму , которая должна быть выдана в момент , привести к моменту , то мы получим сумму . Поэтому если проценты на капитал могут быть выданы заранее, в момент получения займа, то эти проценты, выплачиваемые вперед, составляют от суммы займа . Величина называется эффективной учетной ставкой за единицу времени.

Учетная ставка 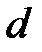может быть выражена и через интенсивность процентов 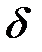и коэффициент дисконтирования :

.

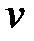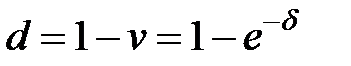Предположим теперь, что сумма 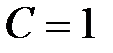дается в долг на время 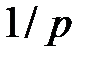с заблаговременной выплатой процентов. Эффективная процентная ставка равна 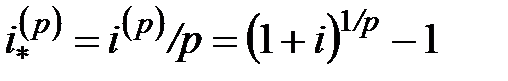. Именно эта сумма должна быть выплачена в момент 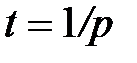в виде процентов. Если ее привести к моменту 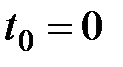, то она превращается в сумму 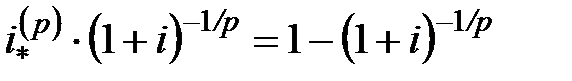. Поскольку 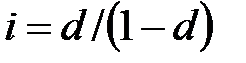, для эффективной учетной ставки 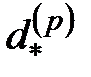за время 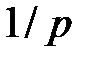имеем формулу

.

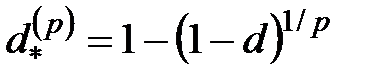Тем не менее, в финансовой математике принято функционировать не с эффективными (т.е реальными) учетными ставками за время 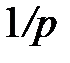, а с номинальными (т.е. условными, не существующими реально) учетными ставками

.

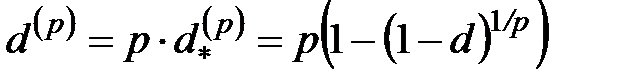Величину 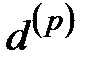называют номинальной учетной ставкой, начисляемой с частотой .

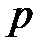Оценивание серии платежей

Детерминированные ренты

С точки зрения приложений к страхованию и пенсионным схемам наиболее значимой является задача определения нынешней стоимости 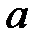серии из 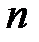выплат величиной 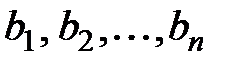соответственно, которые будут приготовлены в некоторые моменты 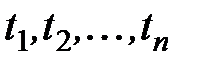в будущем. Величина может рассматриваться, например, как сумма, которую человек должен внести в пенсионный фонд в время заключения договора. Поэтому

.

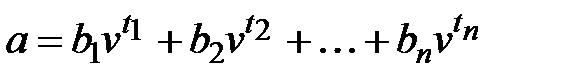Если платеж за пенсии совершается в виде нескольких платежей величиной 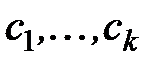, сделанных в моменты 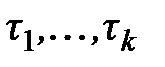, то законное соотношение между взносами 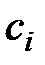и пенсионными выплатами 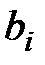находится из принципа эквивалентности обязательств:

.

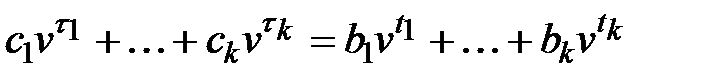Левая часть формулы формулирует современную ценность всех взносов в пенсионный фонд или страховую компанию, а правая – современную стоимость всех пенсионных выплат.

Описанная таким образом всеобщая модель детерминированной пенсионной схемы на практике обыкновенно не применяется. действительно используются схемы, которые обладают той или иной формой регулярности как по величине взносов и выплат, так и по моментам реализации этих платежей. Особо значимым является случай серии платежей фиксированной величины, производящиеся через равные промежутки времени фиксированное число раз. Такие серии платежей обычно называют постоянными рентами или просто рентами.

Часто полезно знать стоимость ренты не в начальный момент времени, а в конце последнего платежного периода. Эту стоимость можно истолковывать как общую сумму, скопленную на банковском счете после серии регулярных взносов. Ее помечают так же, как и приведенную стоимость в начальный момент, но с заменой буквы 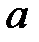на букву .

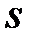Таким образом, 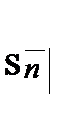– это приведенная стоимость запаздывающей ренты в момент 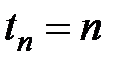последнего платежа, а 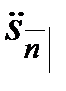– это приведенная стоимость упреждающей ренты в момент 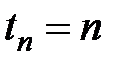, т.е. спустя единицу времени после последнего платежа.

Формулы для накоплени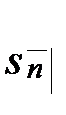й и 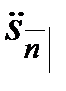можно получить непосредственно, приведя каждый из 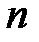платежей к моменту 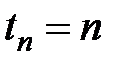и затем складывая полученные значения:

,

.

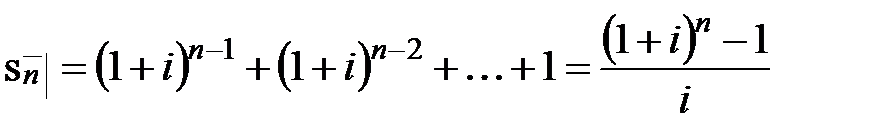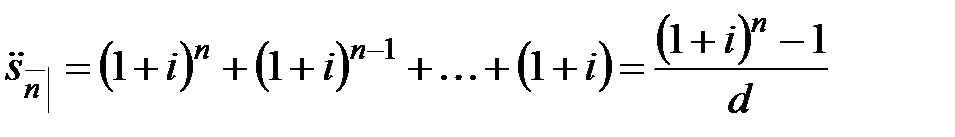Рассмотрим 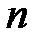последовательных промежутков времени 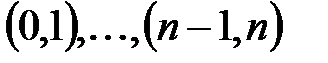. Под моментом 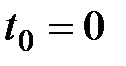как обычно будем подразумевать настоящий момент, а в качестве единичного промежутка будем рассматривать один год.

Разобьем каждый из 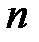единичных промежутков на 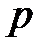равных частей длиной 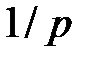каждая.

Серия из 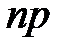выплат, каждая величиной 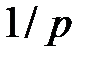, сделанных в конце этих подпромежутков, т.е. в моменты

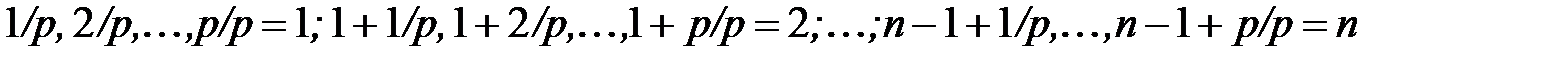
называется запаздывающей рентой, выплачиваемой с частотой 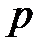. Ее стоимость в настоящий момент времени 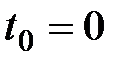обозначается 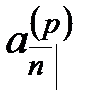, а стоимость в момент 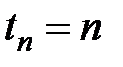последнего платежного периода называется накоплением и обозначается .

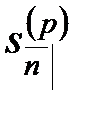Серия из 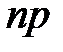выплат, каждая величиной 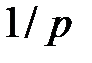, сделанных в начале этих подпромежутков, т.е. в моменты

,

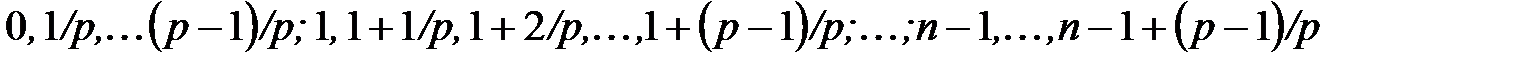называется упреждающей рентой, выплачиваемой с частотой 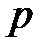. Ее стоимость в настоящий момент времени 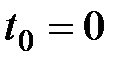обозначается 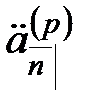, а стоимость в момент 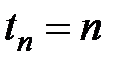последнего платежного периода называется накоплением и обозначается .

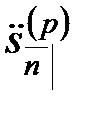Величины 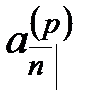и 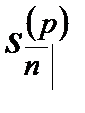, так же как и величины 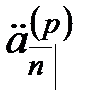и 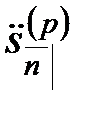, оценивают одну и ту же серию платежей, но в разные моменты времени. Поэтому они связаны соотношениями:

, ,

, ,

.

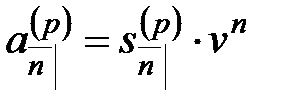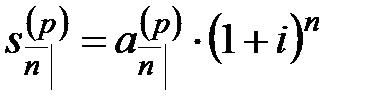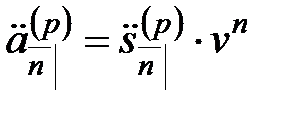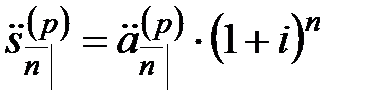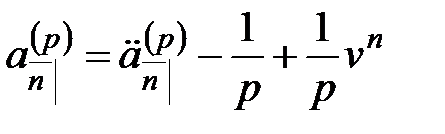Рассмотрим в качестве единичного отрезка времени 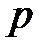-ю долю первоначального единичного отрезка (например, если 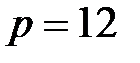и исходный единичный промежуток времени был один год, то новым единичным отрезком времени будет один месяц). Эффективная процентная ставка для этого нового единичного отрезка равна 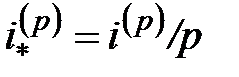, где 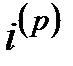– номинальная процентная ставка для основного единичного промежутка, начисляемая с частотой 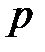. Соответственно, новая учетная ставка равна 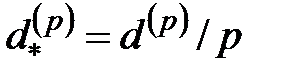, а новое значение коэффициента дисконтирования есть .

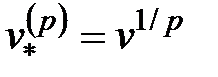Теперь на упреждающую ренту, выплачиваемую с частотой 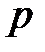на промежутке 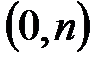, можно смотреть как на обычную упреждающую ренту, выплачиваемую на промежутке 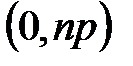. Поскольку каждая выплата равна 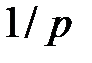, то имеем:

,

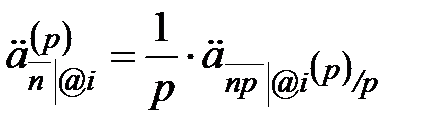где символ 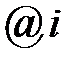указывает эффективную процентную ставку на промежутке, который рассматривается в качестве единичного. Отсюда следует, что:

.

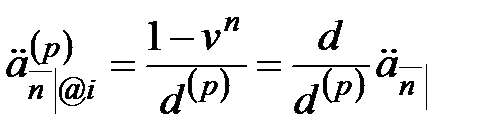Для 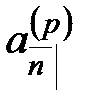верна аналогичная формула:

.

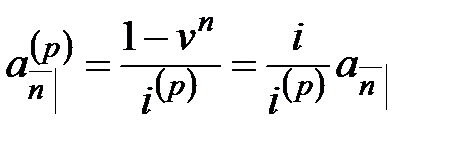Рассмотрим теперь упреждающую и запаздывающую ренты, которые выплачиваются с частотой 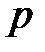на промежутке 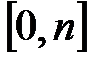, и предположим, что 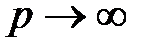. Тогда

,

.

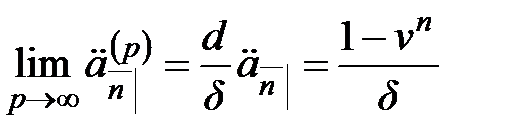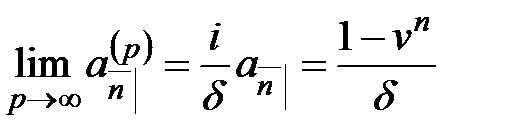Если 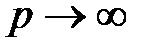, то мы имеем дело с большим числом малых платежей (величиной 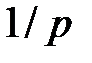каждый), совершаемых через малые промежутки времени 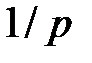. В пределе при 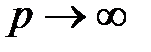можно рассматривать поступление средств как непрерывный процесс, подобный течению жидкости. При этом в пределе различие между платежами в начале и в конце промежутков исчезнет. Непрерывный поток платежей называется непрерывно выплачиваемой рентой. Приведенная стоимость непрерывного потока платежей в момент 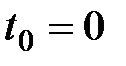обозначается .

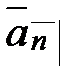Отталкиваясь, от выше сказанного, нужно отметить, что вышеуказанный математический аппарат, а именно, теория вероятностей, математической статистики, финансовой математики являются основой для расчета показателей страховой деятельности. Более того они необходимы для анализа этих показателей, принятия управленческих решений и прогноза.