Гармоническим осциллятором называется система, совершающая колебания описываемые уравнением вида:
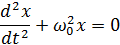
Пружинный маятник – груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы 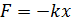 .
.
Физический маятник – твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающую с центром масс тела.
Математический маятник – идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести.
Описание колебаний маятников
| Система | Закон движения, дифференциальное уравнение | Решение дифференциального уравнения | Циклическая частота, 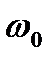
| Период, Т | |||
| Пружинный маятник | 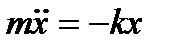 , , 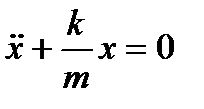 или или 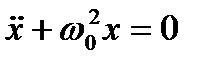
| 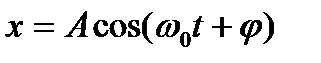
| 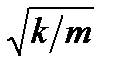
| 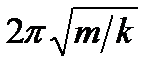
| |||
| k – жесткость пружины, т – масса колеблющегося груза | |||||||
| Математический маятник | 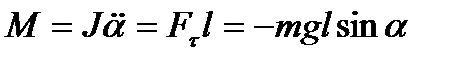 , , 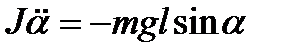 ; при малых колебаниях ; при малых колебаниях 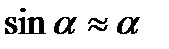 , ,
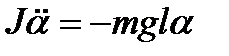 ; ; 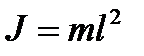 , , 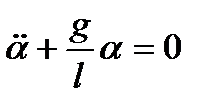 или или 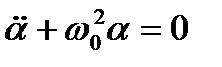
| 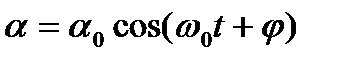
| 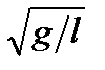
| 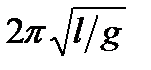
| |||
M – момент возвращающей силы, J – момент инерции маятника, 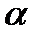 - угол отклонения маятника из положения равновесия, - угол отклонения маятника из положения равновесия, 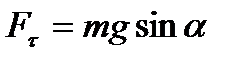 - возвращающая сила, l – длина маятника, g – ускорение свободного падения, - возвращающая сила, l – длина маятника, g – ускорение свободного падения, 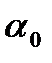 - амплитуда (наибольший угол, на который отклоняется маятник из положения равновесия), m – масса маятника - амплитуда (наибольший угол, на который отклоняется маятник из положения равновесия), m – масса маятника
| |||||||
| Физический маятник | 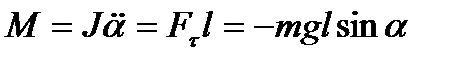 , , 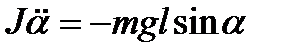 ;
при малых колебаниях ;
при малых колебаниях 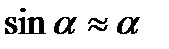 , , 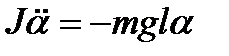 ; ;
 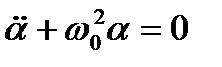
| 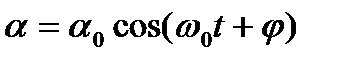
| 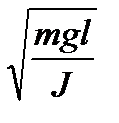
| 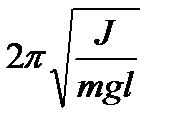
| |||
M – момент возвращающей силы, J – момент инерции маятника относительно оси, проходящей через точку подвеса О, 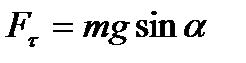 - возвращающая сила, - возвращающая сила, 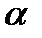 - угол отклонения маятника из положения равновесия, l=ОС – расстояние между точкой подвеса и центром масс маятника, - угол отклонения маятника из положения равновесия, l=ОС – расстояние между точкой подвеса и центром масс маятника, 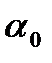 - амплитуда (наибольший угол, на который отклоняется маятник из положения равновесия), m – масса маятника, g – ускорение свободного падения. - амплитуда (наибольший угол, на который отклоняется маятник из положения равновесия), m – масса маятника, g – ускорение свободного падения.
| |||||||
Сложение гармонических колебаний одного направления
и одинаковой частоты
| Сложение колебаний | 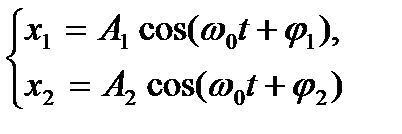
| Для сложения используется метод вращающегося вектора амплитуды
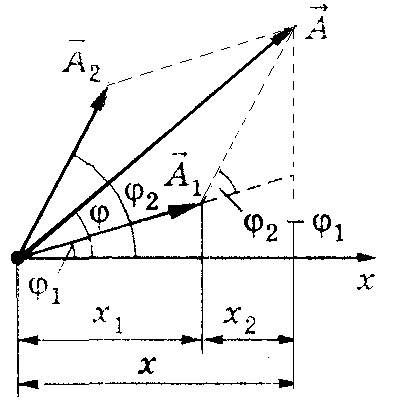
|
| Уравнение результирующего колебания | 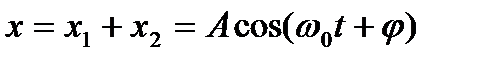
| |
| Амплитуда результирующего колебания | 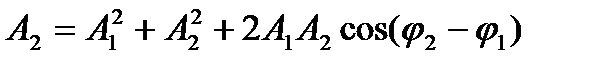
| Векторы 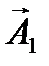 и и 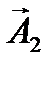 вращаются с одинаковой угловой скоростью вращаются с одинаковой угловой скоростью 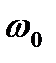 , поэтому разность фаз , поэтому разность фаз 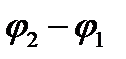 между ними остается постоянной между ними остается постоянной
|
| Начальная фаза | 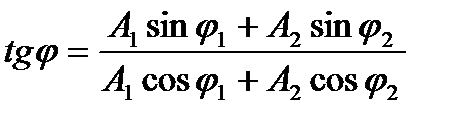
|
Проанализируем выражение для амплитуды результирующего колебания.
1) 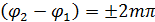 (m=0,1,2,…), тогда
(m=0,1,2,…), тогда 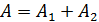 , т.е. амплитуда результирующего колебания равна сумме амплитуд складываемых колебаний.
, т.е. амплитуда результирующего колебания равна сумме амплитуд складываемых колебаний.
2) 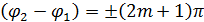 (m=0,1,2,…), тогда
(m=0,1,2,…), тогда 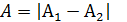 , т.е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний.
, т.е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний.
 2015-08-12
2015-08-12 634
634








