Воздушный зазор δ1
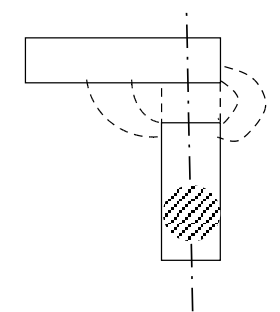
Так как магнитопровод имеет цилиндрическую форму, вблизи зазоров, применяем формулу для цилиндрических полюсов.
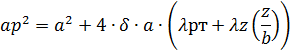
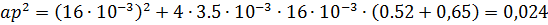
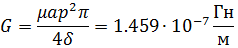
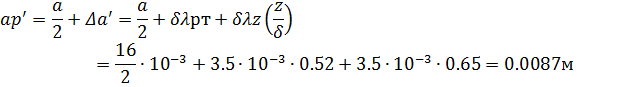
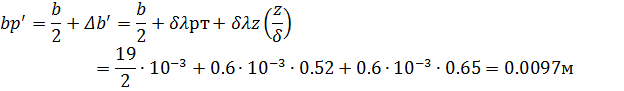
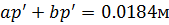
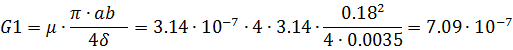
G
Λ(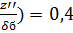 - определяется по графику П5, рис.1,13 уч. «Основы теории Электрических аппаратов»
- определяется по графику П5, рис.1,13 уч. «Основы теории Электрических аппаратов»
Расчет проводимости в промежуточном положении якоря δпр1=(0,3÷0,4)δн
δпр=1.4мм
m1пр= 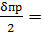 0.7мм
0.7мм
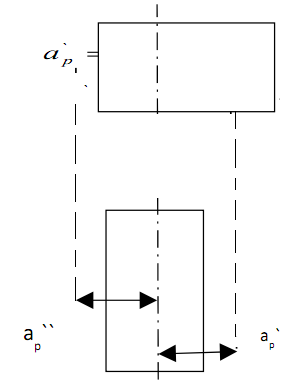
Фигура 1 - цилиндр высотой δ1 и диаметром d
G1= 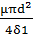 =
= 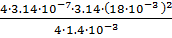 =3.195
=3.195  10-6 Гн
10-6 Гн
Фигура 2 – ¼ цилиндра, длиной l2
G2=μ0  0.52
0.52  l2=
l2= 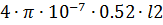 , где l2=
, где l2= 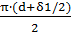 =
= 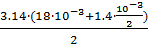 0.021 м
0.021 м
G2= 2.282  10-7 Гн
10-7 Гн
Фигура 3 – четверть полого цилиндра длиной l3, где l3= 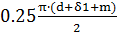 =
= 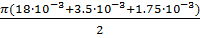 =0.0073 м
=0.0073 м
G3= μ0  0,26
0,26  l3=4
l3=4 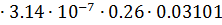 = 2.326
= 2.326  10-9 Гн
10-9 Гн
Фигура 4 полуцилиндр
G4= 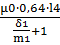 =
= 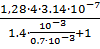 =1,142
=1,142  10-8 Гн
10-8 Гн
Где l4= 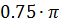 (d +m1+δ1
(d +m1+δ1  )=
)= 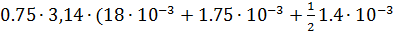 = 0.043м
= 0.043м
Фигура 5половина полого цилиндра
G5= 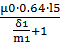 =
= 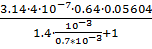 =2.284
=2.284  10-8 Гн
10-8 Гн
Где l5=0.75  2
2  π
π  (d +m1+δ1
(d +m1+δ1 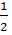 )-l5=
)-l5= 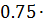 2
2 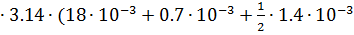 =0.085 м
=0.085 м
GδΣ = G1 + G2 + G3 + G4 + G5
GδΣ = 3.245  10-7 Гн
10-7 Гн
Проводимость воздушного зазора δ2 в промежуточном положении якоря
δ2пр0,4  δ2=0.24
δ2=0.24  10-3м
10-3м
m2пр= δ2пр/2=0,12  10-3 м
10-3 м
Фигура 1- призма высотой δ2 и основанием a-b
G1=μ0 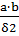 =
= 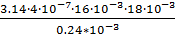 =1.507
=1.507  10-6 Гн
10-6 Гн
Фигура 2- половина цилиндра радиуса δ2
G2=μ0  0.26
0.26  b=3.14
b=3.14 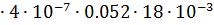 = 5,58
= 5,58  10-9 Гн
10-9 Гн
Фигура 3— четверть полого цилиндра
G3= μ0 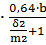 =4
=4 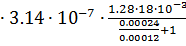 = 4.823
= 4.823  10-9 Гн
10-9 Гн
Фигура 4 – четверть цилиндра диаметром δ 2 длиной b;
G4=μ0  0.52
0.52  b=3.14
b=3.14 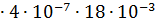 = 1,18
= 1,18  10—8 Гн
10—8 Гн
Фигура 5-– четверть полого цилиндра,
G5= μ0 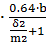 =4
=4 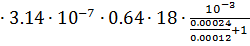 = 4.823
= 4.823  10-9 Гн
10-9 Гн
Фигура 6- полуцилиндр диаметра δ2 длиной а;
G6= μ0  0.26
0.26  a=4
a=4 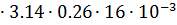 = 5.23
= 5.23  10-9 Гн
10-9 Гн
Фигура 7- половина полого цилиндра длиной а;
G7= μ0 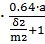 =4
=4 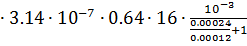 = 4.287
= 4.287  10-9 Гн
10-9 Гн
Фигура 8- сферический квадрант;
G8= μ0  0.088
0.088  δ2=4
δ2=4 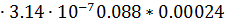 =9.646
=9.646  10-11 Гн
10-11 Гн
Фигура 9- квадрант сферической оболочки;
G9= 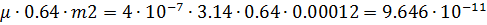
Полная проводимость воздушного зазора есть сумма всех частичных Gδ2 = G1 + G2 + G3 + G4 + G5 + 2G6 + 2G7 + 4G8 + 4G9,
Gδ2= 1.554  10-6 Гн
10-6 Гн
Расчет проводимости в промежуточном положении якоря δпр1=0.1δ
δпр=0.1мм
m1пр= 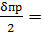 0.05мм
0.05мм
Фигура 1 - цилиндр высотой δ1 и диаметром d
G1= 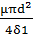 =
= 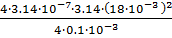 =9.127
=9.127  10-8 Гн
10-8 Гн
Фигура 2 – ¼ цилиндра, длиной l2
G2=μ0  0.52
0.52  l2=
l2= 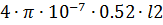 , где l2=
, где l2= 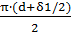 =
= 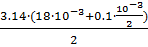 0.024 м
0.024 м
G2= 2.282  10-7 Гн
10-7 Гн
Фигура 3 – четверть полого цилиндра длиной l3, где l3= 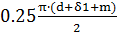 =
= 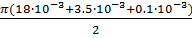 =0.0078 м
=0.0078 м
G3= μ0  0,26
0,26  l3=4
l3=4 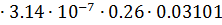 = 2.576
= 2.576  10-9 Гн
10-9 Гн
Фигура 4 полуцилиндр
G4= 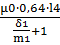 =
= 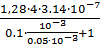 =1,224
=1,224  10-8 Гн
10-8 Гн
Где l4= 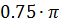 (d +m1+δ1
(d +m1+δ1  )=
)= 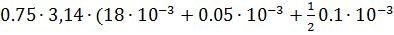 = 0.046м
= 0.046м
Фигура 5половина полого цилиндра
G5= 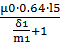 =
= 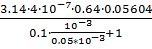 =2.48
=2.48  10-8 Гн
10-8 Гн
Где l5=0.75  2
2  π
π  (d +m1+δ1
(d +m1+δ1 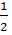 )-l5=
)-l5= 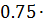 2
2 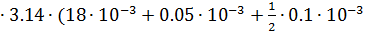 =0.091 м
=0.091 м
GδΣ = G1 + G2 + G3 + G4 + G5
GδΣ = 2.829  10-7 Гн
10-7 Гн
Проводимость воздушного зазора δ2 в конечном положении якоря
δ2пр0,4  δ2=0.1
δ2=0.1  10-3м
10-3м
m2пр= δ2пр/2=0,5  10-3 м
10-3 м
Фигура 1- призма высотой δ2 и основанием a-b
G1=μ0 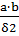 =
= 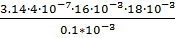 =3.617
=3.617  10-6 Гн
10-6 Гн
Фигура 2- половина цилиндра радиуса δ2
G2=μ0  0.26
0.26  b=3.14
b=3.14 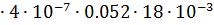 = 5,58
= 5,58  10-9 Гн
10-9 Гн
Фигура 3— четверть полого цилиндра
G3= μ0 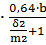 =4
=4 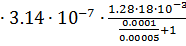 = 4.823
= 4.823  10-9 Гн
10-9 Гн
Фигура 4 – четверть цилиндра диаметром δ 2 длиной b;
G4=μ0  0.52
0.52  b=3.14
b=3.14 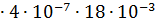 = 1,18
= 1,18  10—8 Гн
10—8 Гн
Фигура 5-– четверть полого цилиндра,
G5= μ0 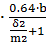 =4
=4 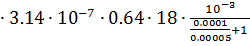 = 4.823
= 4.823  10-9 Гн
10-9 Гн
Фигура 6- полуцилиндр диаметра δ2 длиной а;
G6= μ0  0.26
0.26  a=4
a=4 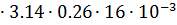 = 5.23
= 5.23  10-9 Гн
10-9 Гн
Фигура 7- половина полого цилиндра длиной а;
G7= μ0 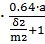 =4
=4 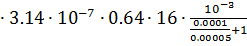 = 4.287
= 4.287  10-9 Гн
10-9 Гн
Фигура 8- сферический квадрант;
G8= μ0  0.088
0.088  δ2=4
δ2=4 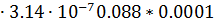 =1.105
=1.105  10-11 Гн
10-11 Гн
Фигура 9- квадрант сферической оболочки;
G9= 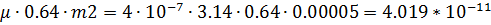
Полная проводимость воздушного зазора есть сумма всех частичных Gδ2 = G1 + G2 + G3 + G4 + G5 + 2G6 + 2G7 + 4G8 + 4G9,
Gδ2= 3.664  10-6 Гн
10-6 Гн
Проводимость по путям рассеивания
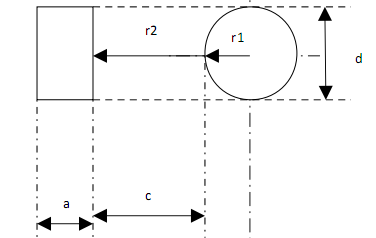 |
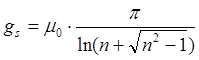 , где n =
, где n = 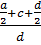 =
= 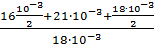 =2.11
=2.11
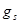 =3.14
=3.14 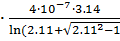
gs= 2.86 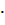 10-6
10-6
Gsпр= 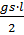 =2.64
=2.64 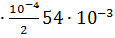 =7.723
=7.723 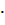 10-8 Гн
10-8 Гн
 2015-08-12
2015-08-12 350
350








