δпр=3,5мм
m1пр= 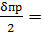
Расчет проводимости δ1
Фигура 1 - цилиндр высотой δ1 и диаметром d
G1= 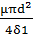 =
= 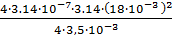 =9.127
=9.127  10-8 Гн
10-8 Гн
Фигура 2 – ¼ цилиндра, длиной l2
G2=μ0  0.52
0.52  l2=
l2= 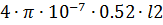 , где l2=
, где l2= 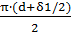 =
= 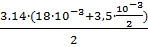 0.027 м
0.027 м
G2= 1.788  10-8 Гн
10-8 Гн
Фигура 3 – четверть полого цилиндра длиной l3, где l3= 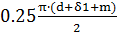 =
= 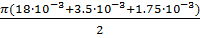 =0.009 м
=0.009 м
G3= μ0  0,26
0,26  l3=4
l3=4 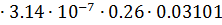 = 1.013
= 1.013  10-8 Гн
10-8 Гн
Фигура 4 полуцилиндр
G4= 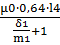 =
= 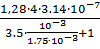 =1,992
=1,992  10-8 Гн
10-8 Гн
Где l4= 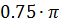 (d +m1+δ1
(d +m1+δ1  )=
)= 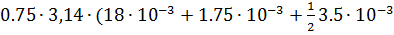 = 0.051м
= 0.051м
Фигура 5половина полого цилиндра
G5= 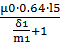 =
= 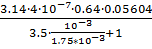 =2.398
=2.398  10-8 Гн
10-8 Гн
Где l5=0.75  2
2  π
π  (d +m1+δ1
(d +m1+δ1 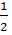 )-l5=
)-l5= 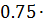 2
2 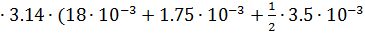 =0.101 м
=0.101 м
GδΣ = G1 + G2 + G3 + G4 + G5
GδΣ =1.576  10-7 Гн
10-7 Гн
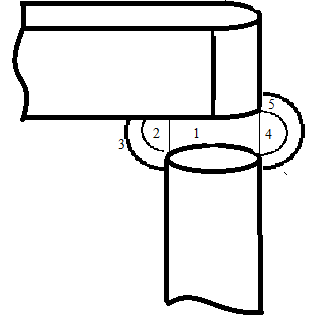
Расчет проводимости технологического зазора Δ:
GΔ= 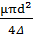 =
= 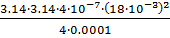 = 3.19
= 3.19  10-7 Гн
10-7 Гн
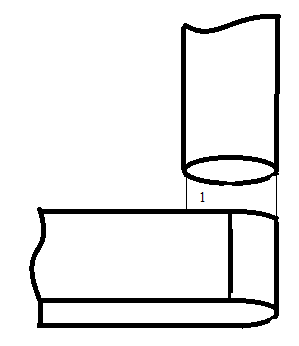
Расчет проводимости δ2:
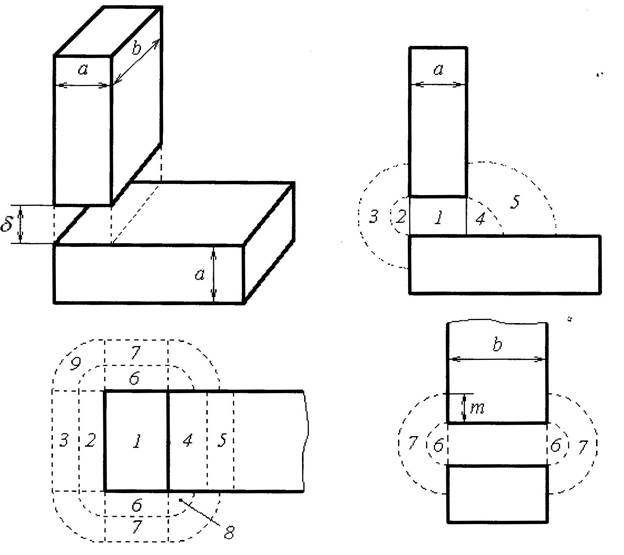
Параметр m2=0.5  δ2=0.0003 м
δ2=0.0003 м
Фигура 1- призма высотой δ2 и основанием a-b
G1=μ0 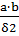 =
= 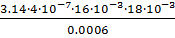 =6,029
=6,029  10-7 Гн
10-7 Гн
Фигура 2- половина цилиндра радиуса δ2
G2=μ0  0.26
0.26  b=3.14
b=3.14 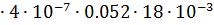 = 5,58
= 5,58  10-9 Гн
10-9 Гн
Фигура 3— четверть полого цилиндра
G3= μ0 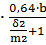 =4
=4 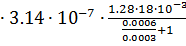 = 4.82
= 4.82  10-9 Гн
10-9 Гн
Фигура 4 – четверть цилиндра диаметром δ 2 длиной b;
G4=μ0  0.52
0.52  b=3.14
b=3.14 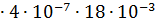 = 1,18
= 1,18  10—8 Гн
10—8 Гн
Фигура 5-– четверть полого цилиндра,
G5= μ0 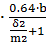 =4
=4 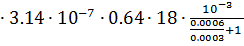 = 4.8
= 4.8  10-9 Гн
10-9 Гн
Фигура 6- полуцилиндр диаметра δ2 длиной а;
G6= μ0  0.26
0.26  a=4
a=4 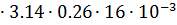 = 5.23
= 5.23  10-9 Гн
10-9 Гн
Фигура 7- половина полого цилиндра длиной а;
G7= μ0 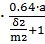 =4
=4 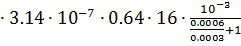 = 4.29
= 4.29  10-9 Гн
10-9 Гн
Фигура 8- сферический квадрант;
G8= μ0  0.088
0.088  δ2=4
δ2=4 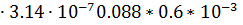 =6.62
=6.62  10-11 Гн
10-11 Гн
Фигура 9- квадрант сферической оболочки;
G9= 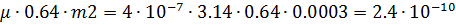
Полная проводимость воздушного зазора есть сумма всех частичных Gδ2 = G1 + G2 + G3 + G4 + G5 + 2G6 + 2G7 + 4G8 + 4G9,
Gδ2= 6.5  10-7 Гн
10-7 Гн
 2015-08-12
2015-08-12 633
633








