Определим напряжённость поля в точке 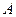 , расположенной на оси кольца на расстоянии
, расположенной на оси кольца на расстоянии 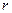 от его центра.
от его центра.

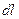
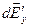
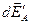
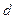
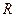
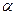
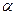
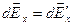
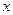
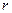
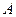
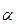
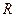
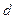
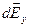
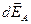
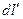
Линейная плотность заряда на кольце:
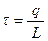 ,
,
где 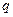 – заряд кольца;
– заряд кольца;
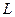 – длина кольца.
– длина кольца.
Рассмотрим малый участок кольца 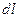 .
.
Его заряд:
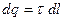 .
.
Расстояние от любого участка 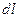 кольца до точки
кольца до точки 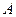 :
:
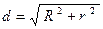 ,
,
где 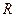 – радиус кольца.
– радиус кольца.
Участок 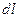 создаёт в точке
создаёт в точке 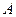 напряжённость:
напряжённость:
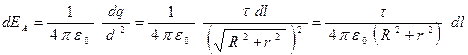 ,
,
где 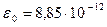 Ф/м – электрическая постоянная.
Ф/м – электрическая постоянная.
Вектор напряжённости 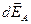 разложим на две составляющие – перпендикулярную плоскости кольца
разложим на две составляющие – перпендикулярную плоскости кольца 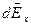 и параллельную плоскости кольца
и параллельную плоскости кольца 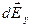 :
:
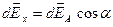 ,
, 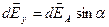 ,
,
где 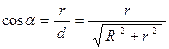 .
.
Любые два противоположных участка будут создавать в точке 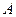 напряжённости
напряжённости 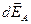 , составляющие которых
, составляющие которых 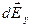 и
и 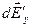 будут равны по величине и противоположны по направлению, и которые попарно компенсируются. Составляющая
будут равны по величине и противоположны по направлению, и которые попарно компенсируются. Составляющая 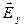 результирующей напряжённости
результирующей напряжённости 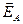 , создаваемой в точке
, создаваемой в точке 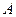 всем кольцом, будет равна 0, поэтому:
всем кольцом, будет равна 0, поэтому:
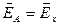 .
.
По принципу суперпозиции имеем:
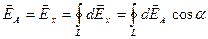 .
.
Поскольку все векторы 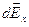 направлены вдоль одной прямой
направлены вдоль одной прямой 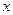 , то векторную сумму можно заменить алгебраической:
, то векторную сумму можно заменить алгебраической:
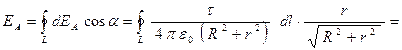
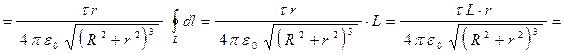
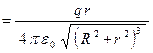 .
.
Тогда сила, с которой действует кольцо на точечный заряд 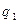 , находящийся в точке
, находящийся в точке 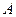 (поскольку заряды
(поскольку заряды 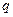 и
и 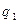 одного знака, то это сила отталкивания):
одного знака, то это сила отталкивания):
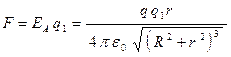 .
.
1) 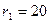 см.
см.
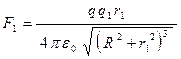 ;
;
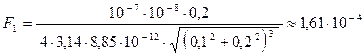 Н
Н 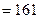 мкН.
мкН.
2) 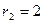 см.
см.
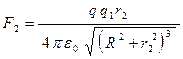 ;
;
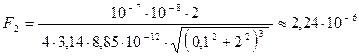 Н
Н 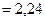 мкН.
мкН.
Заметим, что поскольку 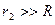 , то кольцо в этом случае можно считать точечным зарядом и силу взаимодействия найти по закону Кулона:
, то кольцо в этом случае можно считать точечным зарядом и силу взаимодействия найти по закону Кулона:
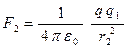 ;
;
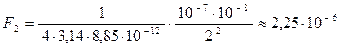 Н
Н 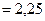 мкН.
мкН.
Ответ: 1) 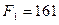 мкН; 2)
мкН; 2) 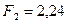 мкН.
мкН.
308. С какой силой (на единицу длины) взаимодействуют две заряженные бесконечно длинные параллельные нити с одинаковой линейной плотностью заряда, равной 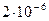 Кл/м, находящиеся на расстоянии 4 см друг от друга?
Кл/м, находящиеся на расстоянии 4 см друг от друга?
| Дано: | |
 Кл/м Кл/м | |
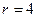 см см | 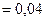 м м |
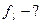 |
 2015-08-21
2015-08-21 1376
1376







