Allowable mean pressure [p], in MPa
| n1, rpm | Chain pitch, mm | |||||||
| 12.7 | 15.875 | 19.05 | 25.4 | 31.75 | 38.1 | 44.45 | 50.8 | |
| - | - | |||||||
| - | - | - | ||||||
| - | - | - | - |
8.6. Determine the chain pitch
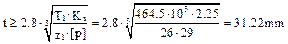 ,
,
where T1 is in N×m.
Round off the pitch to the nearest standard value according to the table 8.1. In our case assume t = 31.75 mm.
8.7. Specify the allowable mean pressure according to table 8.1 by interpolation [p]. On multiplying it by
Kp = 1 + 0.01·(z1-17) = 1 + 0.01·(26-17)=1.09 we get finite magnitude of [p] = 29·1.09=31.61MPa
8.8. Determine the effective mean pressure.
For that we
- find chain speed
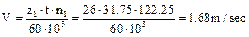 ;
;
- find turning (tangential) force
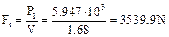 ;
;
- look up the projected hinge area Sh using table 8.2. In our case Sh=262 mm2
Then the effective mean pressure
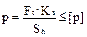 .
.
If this inequality is not right it is necessary to increase the pitch t.
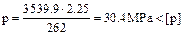 ;
;
inequality is right.
8.9. Determine the number of links in the chain
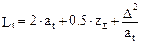 ,
,
where 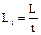 is the chain length in pitches;
is the chain length in pitches; 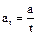 ; a» (30…50)·t; zS = z1 + z2;
; a» (30…50)·t; zS = z1 + z2; 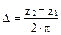 . Round off obtained magnitude to even integer numeral.
. Round off obtained magnitude to even integer numeral.
In our case: at = 45; zS = 26 + 65 = 91; 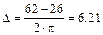 ;
;
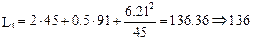
8.10. Specify the centre distance
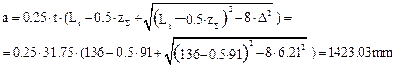
The slack side of the chain should have a slight sag f» 0.01·a, for which purpose the design centre distance is reduced by 0.2 to 0.4 %.
|
|
|
Assume that a = 1418.76 mm.
8.11. Determine the pitch diameters
- of the driving sprocket 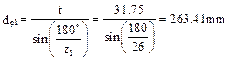 ;
;
- of the driven sprocket 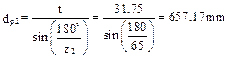 .
.
8.12. Determine the addendum diameters
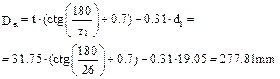
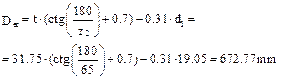
where d1 is the roller diameter (table 8.2).
8.13. Determine the dedendum diameter
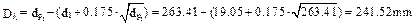 ,
,
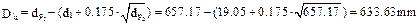 .
.
 2015-08-21
2015-08-21 474
474