Барометрична формула. Розподіл Больцмана

У разі обґрунтування розподілу молекул за швидкостями і кінетичними енергіями ми вважали, що зовнішні сили на молекули газу не діють. А як поводиться газ, що перебуває у потенціальному полі? Розглянемо це на прикладі земної атмосфери. Відомо, що атмосферний тиск зумовлений силами гравітаційного притягання, які діють на молекули повітря з боку Землі. Вважатимемо, що атмосферне повітря перебуває у стаціонарному стані, а його температура всюди однакова. За цих умов рівноважний стан довільного виділеного об’єму повітря забезпечений тим, що вага повітря зрівноважена силою Архімеда, яка зумовлена різницею тисків, що діють на нижню і верхню основи виділеного об’єму. Водночас молекули повітря перебувають у хаотичному безупинному тепловому русі. Сукупна дія сили тяжіння і теплового руху молекул спричиняє нерівномірність розподілу густини атмосфери з висотою, отже атмосферний тиск з висотою h знижується. Цю залежність виражає барометрична формула, уперше отримана П. Лапласом 1821 р.:

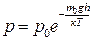, (2.25)

де р ₀ – атмосферний тиск на рівні моря (h =0).

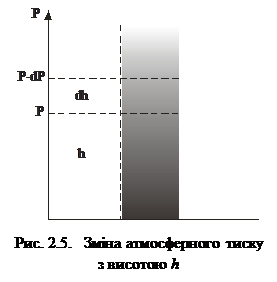
Для доведення (2.25) розглянемо статичний вертикальний атмосферний стовп повітря висоти h (рис. 2.5). Нехай на висоті h тиск повітря становить р, тоді на висоті h + dh тиск дорівнюватиме

р - dp. Оскільки в шарі товщиною dh густину повітря можна вважати сталою, то приріст тиску

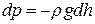. (2.26)

Якщо тепер скористатись рівнянням стану газу p = nkT і врахувати, щ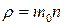о , то 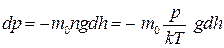, звідки

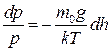. (2.27)

Проінтегруємо (2.27) в межах від р ₀ до р і від 0 до h, отримаємо формулу Лапласа (2.25). Якщо тепер знову скористатись рівнянням стану газу 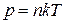то (2.25) можна звести до вигляду

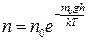, (2.28)

де n – концентрація молекул на висоті h, n ₀ – концентрація молекул на рівні h =0.

Зазначимо, що m ₀ gh – це потенціальна енергія молекул повітря у полі сили земного тяжіння. Больцман довів, що залежність (2.28) характерна для будь-якого газу, який перебуває у потенціальному полі

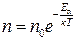. (2.29)

Розподіл Больцмана (2.29) описує рівноважний розподіл за потенціальною енергією молекул газу, що перебувають у зовнішньому потенціальному полі сил.

Якщо концентрація частинок невідома в жодній точці поля, але відома загальна кількість частинок N, то розподіл Больцмана записують у вигляді

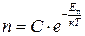. (2.30)

Нормувальний множник С знаходять з умови нормування

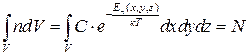, (2.31)

де V – об’єм, у якому містяться частинки.

2.3.3. Розподіл Максвелла – Больцмана

У потенціальному полі координати і швидкості молекул газу незалежні, отже, незалежними є й обидва розподіли – Максвелла та Больцмана. Водночас їх можна об’єднати в один розподіл Максвелла–Больцмана, відповідно до якого кількість молекул, компоненти швидкості яких містяться у проміжках v_x, v_x + dv_x; v_y, v_y + dv_y; v_z, v_z+dv_z, а координати, відповідно, – у проміжках x, x+dx; y, y+dy; z, z+dz,

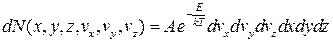, (2.32)

де 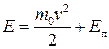– повна енергія частинки; .

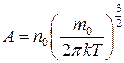Якщо у (2.32) зробити перетворення і перейти до змінних Е _к і Е _п, то

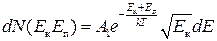. (2.33)

Тут

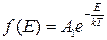(2.34)

– це функція розподілу Максвелла–Больцмана.

2.3.4. Квантові аспекти розподілів. Розподіли Бозе – Айнштайна і Фермі – Дірака

Системи багатьох частинок, для яких застосовні розподіли Максвелла і Больцмана, складаються з частинок, які можна розрізняти за певними ознаками. Якщо ж система складається з однакових нерозрізнюваних частинок, то і їхні статистичні розподіли будуть іншими. З погляду квантової механіки стан мікрочастинки визначений певним набором квантових чисел. Кожному набору квантових чисел відповідає цілком певне значення енергії. Отже, розподіл таких частинок за енергіями зумовлений їхнім розподілом за квантовими станами. Є два квантові статистичні розподіли – Бозе–Айнштайна і Фермі–Дірака. Ці розподіли описують стан систем мікрочастинок, кожна з яких має нульовий або цілий спін, чи напівцілий. Частинки, що мають цілий спін ферміони (це електрони, протони, нейтрони та ін.), а ті, що мають нульовий, – бозонами (це фотони, фонони, мезони та ін.). Різниця між бозе- і фермі-газом полягає в тому, що кількість бозе-частинок з однаковою енергією може бути довільною, тоді як у фермі-газі однакову енергію можуть мати не більше двох частинок з протилежними спінами.

Середню кількість частинок з енергією у проміжку від Е до Е+dE обчислюють за відповідними функціями розподілу:

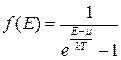– функція розподілу Бозе–Айнштайна, (2.35)

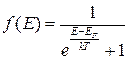– функція розподілу Фермі–Дірака. (2.36)

Зазначимо, що квантові розподіли безпосередньо пов’язані з класичним розподілом Максвелла–Больцмана. Справді, за умови Е >> kТ експонен-ціальний доданок у (2.35) і (2.36) стає суттєво більшим від одиниці, якою можна знехтувати. За цих умов обидва квантові розподіли перетворюються у класичний розподіл Максвелла–Больцмана (2.34).