Статические сети. Воспользуемся следующей моделью однослойной линейной сети
с двухэлементным вектором входа, значения которого находятся в интервале [–1 1],
и нулевым параметром скорости настройки:
% Формирование однослойной статической линейной сети с двумя входами
% и нулевым параметром скорости настройки
net = newlin([–1 1;–1 1],1, 0, 0);
Требуется адаптировать параметры сети так, чтобы она формировала линейную зависимость вида
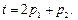
Последовательный способ. Рассмотрим случай последовательного представления обучающей последовательности. В этом случае входы и целевой вектор формируются в виде массива формата cell:
% Массив ячеек векторов входа
P = {[–1; 1] [–1/3; 1/4] [1/2; 0] [1/6; 2/3]};
T = {–1 –5/12 1 1}; % Массив ячеек векторов цели
P1 = [P{:}], T1=[T{:}] % Переход от массива ячеек к массиву double
P1 =
–1 –0.33333 0.5 0.16667
1 0.25 0 0.66667
T1 = –1 –0.41667 1 1
Сначала зададим сеть с нулевыми значениями начальных весов и смещений:
net.IW{1} = [0 0]; % Присваивание начальных весов
net.b{1} = 0; % Присваивание начального смещения
В ППП NNT процедуры адаптации реализуются на основе метода adapt. Для управления процедурой адаптации используется свойство net.adaptFcn, которое задает метод адаптации; для статических сетей по умолчанию применяется метод adaptwb, который позволяет выбирать произвольные функции для настройки весов и смещений. Функции настройки весов и смещений задаются свойствами net.inputWeights{i, j}.learnFcn, net.layerWeights{i, j}.learnFcn и net.biases{i, j}.learnFcn.
Выполним 1 цикл адаптации сети с нулевым параметром скорости настройки:
% Последовательная адаптация сети с входами P и целями T
[net1,a,e] = adapt(net,P,T);
% net1-новая сеть, a-выход, e-ошибка обучения
В этом случае веса не модифицируются, выходы сети остаются нулевыми, поскольку параметр скорости настройки равен нулю и адаптации сети не происходит. Погрешности совпадают со значениями целевой последовательности
net1.IW{1, 1}, a, e
ans = 0 0
a = [0] [0] [0] [0]
e = [–1] [–0.41667] [1] [1]
Зададим значения параметров скорости настройки и весов входа и смещения:
net.IW{1} = [0 0]; % Присваивание начальных весов
net.b{1} = 0; % Присваивание начального смещения
net.inputWeights{1,1}.learnParam.lr = 0.2;
net.biases{1,1}.learnParam.lr = 0;
Нулевое значение параметра скорости настройки для смещения обусловлено тем, что выявляемая зависимость не имеет постоянной составляющей.
Выполним 1 цикл настройки:
[net1,a,e] = adapt(net,P,T);
net1.IW{1, 1}, a, e
ans = 0.34539 –0.069422
a = [0] [–0.11667] [0.11] [–0.091833]
e = [–1] [–0.3] [0.89] [1.0918]
Теперь выполним последовательную адаптацию сети в течение 30 циклов:
% Последовательная адаптация сети с входами P и целями T за 30 циклов
net = newlin([–1 1;–1 1],1, 0, 0);
net.IW{1} = [0 0]; % Присваивание начальных весов
net.b{1} = 0; % Присваивание начального смещения
Зададим значения параметров скорости настройки для весов входа и смещения:
net.inputWeights{1,1}.learnParam.lr = 0.2;
net.biases{1,1}.learnParam.lr = 0;
P = {[–1; 1] [–1/3; 1/4] [1/2; 0] [1/6; 2/3]}; % Массив векторов входа
T = {–1 –5/12 1 1}; % Массив векторов цели
for i=1:30,
[net,a{i},e{i}] = adapt(net,P,T);
W(i,:)=net.IW{1,1};
end
mse(cell2mat(e{30})) % Среднеквадратичная ошибка адаптации
ans = 0.0017176
W(30,:) % Веса после 30 циклов
ans = 1.9199 0.925
cell2mat(a{30})
ans = –0.9944 –0.40855 0.95663 0.93005
cell2mat(e{30})
ans = –0.0055975 –0.0081125 0.043367 0.069947
Построим графики зависимости значений выходов сети и весовых коэффициентов
в зависимости от числа итераций (рис. 3.1):
subplot(3,1,1)
plot(0:30,[[0 0 0 0];cell2mat(cell2mat(a'))],'k') % Рис 3.1,a
xlabel(''), ylabel('Выходы a(i)'),grid
subplot(3,1,2)
plot(0:30,[[0 0]; W],'k') % Рис 3.1,б
xlabel(''), ylabel('Веса входов w(i)'),grid
subplot(3,1,3)
for i=1:30, E(i) = mse(e{i}); end
semilogy(1:30, E,'+k') % Рис. 3.1,в
xlabel(' Циклы'), ylabel('Ошибка'),grid
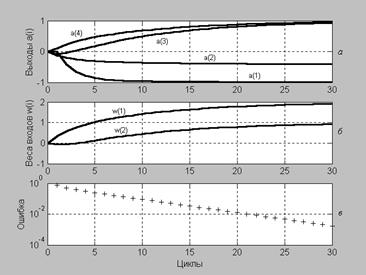
Рис. 3.1
Первый выход тот же, что и при нулевом значении параметра скорости настройки, так как до предъявления сети первого входа никаких модификаций не происходит. Второй выход отличается, так как параметры сети были модифицированы. Веса продолжают
изменяться при подаче нового входа. Если сеть соответствует задаче, корректно заданы обучающие последовательности, начальные условия и параметр скорости настройки,
то в конечном счете погрешность может быть сведена к нулю.
В этом можно убедиться, изучая процесс адаптации, показанный на рис. 3.1. Условие окончания адаптации определяется погрешностью приближения к целевому вектору; в данном случае мерой такой погрешности является среднеквадратичная ошибка mse(e{i}), которая должна быть меньше 0.015.
На рис. 3.1, а показаны выходы нейронов в процессе адаптации сети, на рис. 3.1, б – коэффициенты восстанавливаемой зависимости, которые соответствуют элементам
вектора весов входа, а на рис. 3.1, в – ошибка обучения. Как следует из анализа графиков, за 12 шагов получена ошибка обучения 1.489e–3.
Предлагаем читателю самостоятельно убедиться, что для исследуемой зависимости обучающие последовательности вида
P = {[–1; 1] [–1/2; 1/2] [1/2; –1/2] [1; –1]}; % Массив векторов входа
T = {–1 –1/2 1/2 1}; % Массив векторов цели
не являются представительными.
Групповой способ. Рассмотрим случай группового представления обучающей последовательности. В этом случае входы и целевой вектор формируются в виде массива формата double.
P = [–1 –1/3 1/2 1/6; 1 1/4 0 2/3];
T = [–1 –5/12 1 1];
Используется та же модель статической сети с теми же требованиями к погрешности адаптации. При обращении к М-функции adapt по умолчанию вызываются функции adaptwb и learnwh; последняя выполняет настройку параметров сети на основе алгоритма WH, реализующего правило Уидроу – Хоффа (Widrow – Hoff).
Основной цикл адаптации сети с заданной погрешностью выглядит следующим образом:
% Групповой способ адаптации сети с входами P и целями T
net3 = newlin([–1 1;–1 1],1, 0, 0.2);
net3.IW{1} = [0 0]; % Присваивание начальных весов
net3.b{1} = 0; % Присваивание начального смещения
net3.inputWeights{1,1}.learnParam.lr = 0.2;
P = [–1 –1/3 1/2 1/6; 1 1/4 0 2/3];
T = [–1 –5/12 1 1];
EE = 10; i=1;
while EE > 0.0017176
[net3,a{i},e{i},pf] = adapt(net3,P,T);
W(i,:) = net3.IW{1,1};
EE = mse(e{i});
ee(i)= EE;
i = i+1;
end
Результатом адаптации при заданной погрешности являются следующие значения коэффициентов линейной зависимости, значений выходов нейронной сети, приближающихся к значениям желаемого выхода, а также среднеквадратичная погрешность адаптации:
W(63,:)
ans = 1.9114 0.84766
cell2mat(a(63))
ans = –1.003 –0.36242 1.0172 0.94256
EE = mse(e{63})
EE = 0.0016368
mse(e{1})
ans = 0.7934
Процедура адаптации выходов и параметров нейронной сети иллюстрируется рис. 3.2.
subplot(3,1,1)
plot(0:63,[zeros(1,4); cell2mat(a')],'k') % Рис.3.2,a
xlabel(''), ylabel('Выходы a(i)'),grid
subplot(3,1,2)
plot(0:63,[[0 0]; W],'k') % Рис.3.2,б
xlabel(''), ylabel('Веса входов w(i)'),grid
subplot(3,1,3)
semilogy(1:63, ee,'+k') % Рис.3.2,в
xlabel('Циклы'), ylabel('Ошибка'),grid
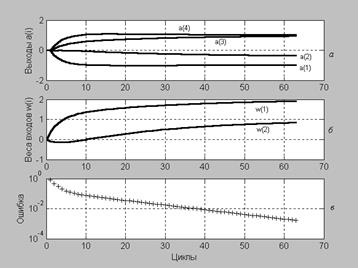
Рис. 3.2
Как следует из анализа графиков, для достижения требуемой точности адаптации требуется 12 шагов. Сравнивая рис. 3.2 и 3.1, можно убедиться, что существует различие в динамике процедур адаптации при последовательном и групповом представлении данных.
Динамические сети. Эти сети характеризуются наличием линий задержки, и для них
последовательное представление входов является наиболее естественным.
Последовательный способ. Обратимся к линейной модели нейронной сети с одним входом и одним элементом запаздывания. Установим начальные условия на линии задержки, а также для весов и смещения равными 0, а параметр скорости настройки равным 0.5:
net = newlin([–1 1],1,[0 1],0.5);
Pi = {0}; % Начальное условие для элемента запаздывания
net.IW{1} = [0 0]; % Значения весов
net.biasConnect = 0; % Значение смещения
Чтобы применить последовательный способ адаптации, представим входы и цели как массивы ячеек:
P = {–1/2 1/3 1/5 1/4}; % Вектор входа
T = { –1 1/6 11/15 7/10}; % Вектор цели
Попытаемся приспособить сеть для формирования нужного выхода на основе следующего соотношения:
y(t) = 2p(t) + p(t–1).
Используем для этой цели М-функцию adapt и основной цикл адаптации сети с заданной погрешностью, как это уже было описано выше:
EE = 10; i = 1;
while EE > 0.0001
[net,a{i},e{i},pf] = adapt(net,P,T);
W(i,:)=net.IW{1,1};
EE = mse(e{i});
ee(i) = EE;
i = i+1;
end
Сеть адаптировалась за 22 цикла. Результатом адаптации при заданной погрешности являются следующие значения коэффициентов линейной зависимости, значений выходов нейронной сети, приближающихся к значениям желаемого выхода, а также среднеквадратичная погрешность адаптации:
W(22,:)
ans = 1.983 0.98219
a{22}
ans = [–0.98955] [0.17136] [0.72272] [0.69177]
EE
EE = 7.7874e–005
Построим графики зависимости выходов системы и весовых коэффициентов от числа циклов обучения (рис. 3.3):
subplot(3,1,1)
plot(0:22,[zeros(1,4); cell2mat(cell2mat(a'))],'k') % Рис.3.3,a
xlabel(''), ylabel('Выходы a(i)'),grid
subplot(3,1,2)
plot(0:22,[[0 0]; W],'k') % Рис.3.3,б
xlabel(''), ylabel('Веса входов w(i)'),grid
subplot(3,1,3)
semilogy(1:22,ee,'+k') % Рис.3.3,в
xlabel('Циклы'), ylabel('Ошибка'),grid
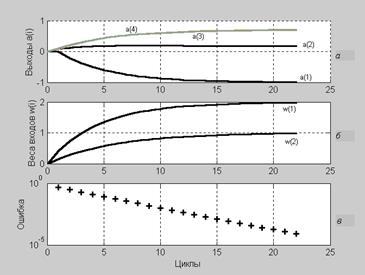
Рис. 3.3
На рис. 3.3, а показаны выходы нейронов в процессе адаптации сети, а на рис. 3.3, б – коэффициенты восстанавливаемой зависимости, которые соответствуют элементам вектора весов входа.
Групповой способ представления обучающего множества для адаптации динамических систем не применяется.
 2015-08-21
2015-08-21 1384
1384
