Примеры радиальных базисных сетей

Демонстрационный пример demorb1 иллюстрирует применение радиальной базисной сети для решения задачи аппроксимации функции от одной переменной.

Представим функцию f (x) следующим разложением:

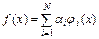, (6.2)

где j_i (x) – радиальная базисная функция.

Тогда идея аппроксимации может быть представлена графически следующим образом. Рассмотрим взвешенную сумму трех радиальных базисных функций, заданных
на интервале [–3 3].

p = –3:.1:3;

a1 = radbas(p);

a2 = radbas(p–1.5);

a3 = radbas(p+2);

a = a1 + a2*1 + a3*0.5;

plot(p,a1,p,a2,p,a3*0.5,p,a) % Рис. 6.6

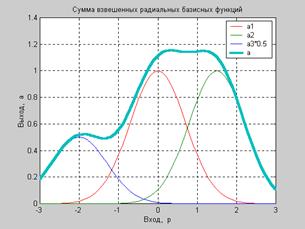Рис. 6.6

Как следует из анализа рис. 6.6 разложение по радиальным базисным функциям обеспечивает необходимую гладкость. Поэтому их применение для аппроксимации произвольных нелинейных зависимостей вполне оправдано. Разложение вида (6.2) может быть реализовано на двухслойной нейронной сети, первый слой которой состоит из радиальных базисных нейронов, а второй – из единственного нейрона с линейной характеристикой, на котором реализуется суммирование выходов нейронов первого слоя.

Приступим к формированию радиальной базисной сети. Сформируем обучающее множество и зададим допустимое значение функционала ошибки, равное 0.01, параметр влияния определим равным 1 и будем использовать итерационную процедуру формирования радиальной базисной сети:

P = –1:.1:1;

T = [–.9602 –.5770 –.0729.3771.6405.6600.4609.1336...

–.2013 –.4344 –.5000 –.3930 –.1647.0988.3072.3960...

.3449.1816 –.0312 –.2189 –.3201];

GOAL = 0.01; % Допустимое значение функционала ошибки

SPREAD = 1; % Параметр влияния

net = newrb(P,T,GOAL,SPREAD); % Создание сети

net.layers{1}.size % Число нейронов в скрытом слое

ans = 6

Для заданных параметров нейронная сеть состоит из шести нейронов и обеспечивает следующие возможности аппроксимации нелинейных зависимостей после обучения.
Моделируя сформированную нейронную сеть, построим аппроксимационную кривую
на интервале [–1 1] с шагом 0.01 для нелинейной зависимости.

plot(P,T,'+k') % Точки обучающего множества

hold on;

X = –1:.01:1;

Y = sim(net,X); % Моделирование сети

plot(X,Y); % Рис. 6.7

Из анализа рис. 6.7 следует, что при небольшом количестве нейронов скрытого слоя радиальная базисная сеть достаточно хорошо аппроксимирует нелинейную зависимость, заданную обучающим множеством из 21 точки.

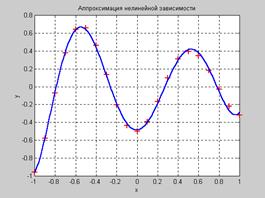Рис. 6.7

В демонстрационных примерах demorb3 и demorb4 исследуется влияние параметра SPREAD на структуру радиальной базисной сети и качество аппроксимации. В демонстрационном примере demorb3 параметр влияния SPREAD установлен равным 0.01. Это означает, что диапазон перекрытия входных значений составляет лишь ±0.01, а поскольку обучающие входы заданы с интервалом 0.1, то входные значения функциями активации не перекрываются.

GOAL = 0.01; % Допустимое значение функционала ошибки

SPREAD = 0.01; % Параметр влияния

net = newrb(P,T,GOAL,SPREAD); % Создание сети

net.layers{1}.size % Число нейронов в скрытом слое

ans = 19

Это приводит к тому, что, во-первых, увеличивается количество нейронов скрытого слоя с 6 до 19, а во-вторых, не обеспечивается необходимой гладкости аппроксимируемой функции:

plot(P,T,'+k') % Точки обучающего множества

hold on;

X = –1:.01:1;

Y = sim(net,X); % Моделирование сети

plot(X,Y); % Рис. 6.8

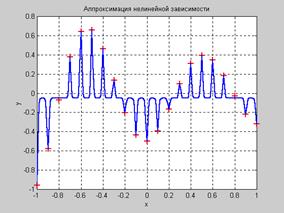Рис. 6.8

Пример demorb4 иллюстрирует противоположный случай, когда параметр влияния SPREAD выбирается достаточно большим (в данном примере – 12 или больше), то все функции активации перекрываются и каждый базисный нейрон выдает значение, близкое к 1, для всех значений входов. Это приводит к тому, что сеть не реагирует на входные значения. Функция newrb будет пытаться строить сеть, но не сможет обеспечить необходимой точности из-за вычислительных проблем.

GOAL = 0.01; % Допустимое значение функционала ошибки

SPREAD = 12; % Параметр влияния

net = newrb(P,T,GOAL,SPREAD); % Создание сети

net.layers{1}.size % Число нейронов в скрытом слое

ans = 21

В процессе вычислений возникают трудности с обращением матриц, и об этом выдаются предупреждения; количество нейронов скрытого слоя устанавливается равным 21,
а точность аппроксимации оказывается недопустимо низкой:

plot(P,T,'+k') % Точки обучающего множества

hold on;

X = –1:.01:1;

Y = sim(net,X); % Моделирование сети

plot(X,Y); % Рис. 6.9

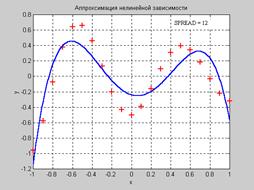Рис. 6.9

Вывод из выполненного исследования состоит в том, что параметр влияния SPREAD следует выбирать большим, чем шаг разбиения интервала задания обучающей последовательности, но меньшим размера самого интервала. Для данной задачи это означает, что параметр влияния SPREAD должен быть больше 0.1 и меньше 2.