Рассмотрим теперь винтовую неустойчивость применительно к установке типа «токамак». В токамаке тороидальное поле (в случае цилиндра с отождествленными концами поле в направлении оси z) существенно превышает полоидальное, 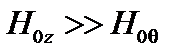 . Плазма занимает центральную часть цилиндра,
. Плазма занимает центральную часть цилиндра, 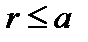 . Вакуум занимает область
. Вакуум занимает область 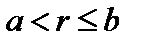 . Следовательно, в энергетический принцип должен включать энергию поверхности и вакуумной области. Энергия поверхности имеет вид
. Следовательно, в энергетический принцип должен включать энергию поверхности и вакуумной области. Энергия поверхности имеет вид
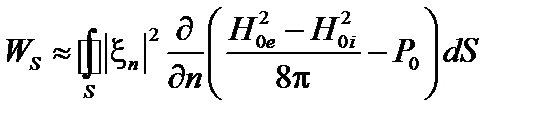 . (3.5.1)
. (3.5.1)
Из условия равновесия 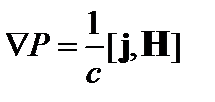 имеем:
имеем:
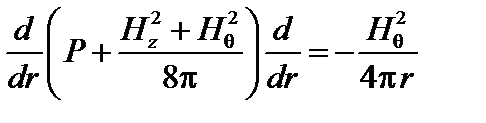 . (3.5.2)
. (3.5.2)
На границе «плазма-вакуум» полоидальное магнитное поле непрерывно, производная 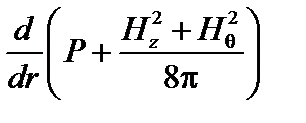 также непрерывна, то есть
также непрерывна, то есть
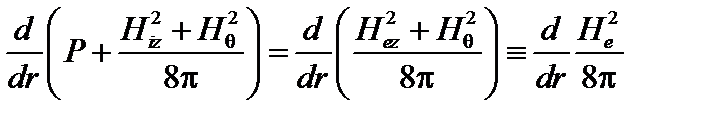 . (3.5.3)
. (3.5.3)
Подставляя (3.5.3) в (3.5.1), находим, что
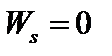 . (3.5.4)
. (3.5.4)
Вычислим теперь вклад 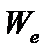 от вакуумной области
от вакуумной области
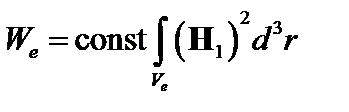 . (3.5.5)
. (3.5.5)
В вакуумной области магнитное поле можно представить как градиент скалярной функции 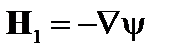 ,
, 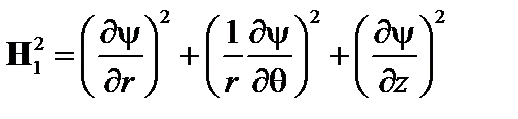 . Разлагая
. Разлагая 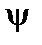 в ряд Фурье по
в ряд Фурье по 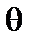 и
и 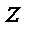 , получаем
, получаем
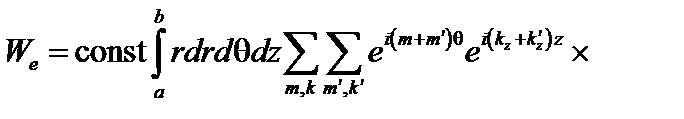
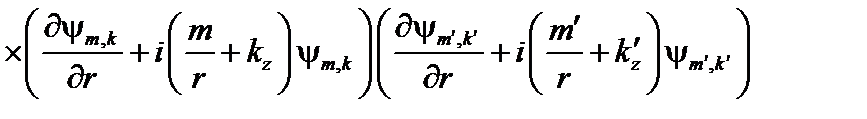 .
.
При интегрировании по 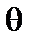 и
и 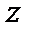 остаются только те члены, для которых
остаются только те члены, для которых 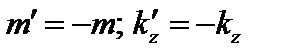 . Тогда
. Тогда
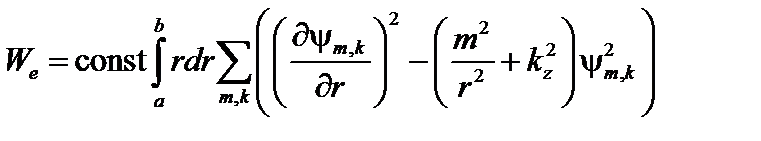 . (3.5.6)
. (3.5.6)
Введем величину 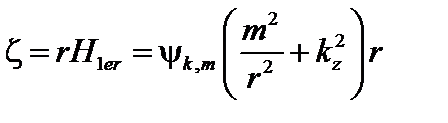 . Подставляя это выражение в (3.5.6), получаем
. Подставляя это выражение в (3.5.6), получаем
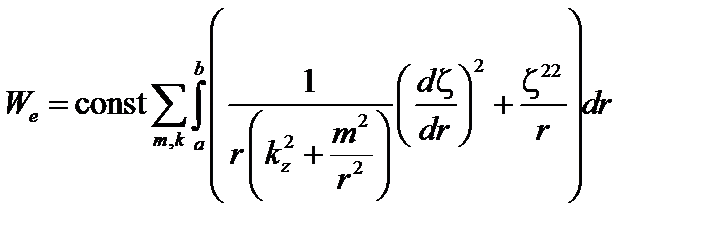 . (3.5.7)
. (3.5.7)
Таким образом, функции 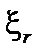 и
и 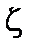 являются решениями уравнений Эйлера:
являются решениями уравнений Эйлера:
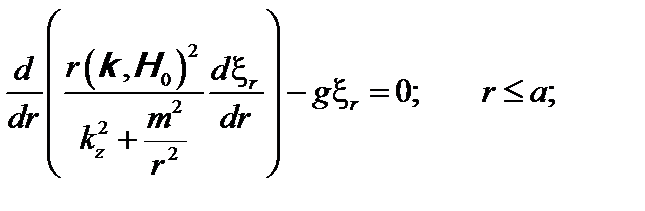 (3.5.8)
(3.5.8)
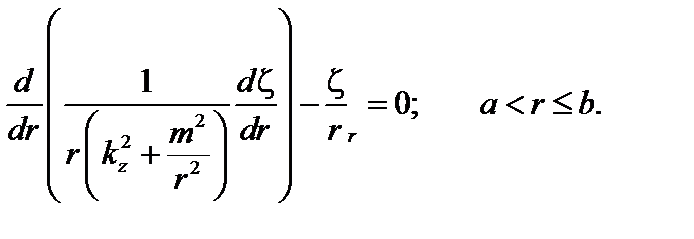 (3.5.9)
(3.5.9)
Решение уравнения (3.5.9) c граничным условием 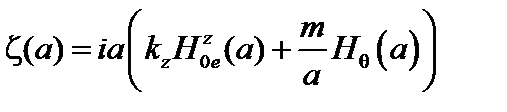 таково:
таково:
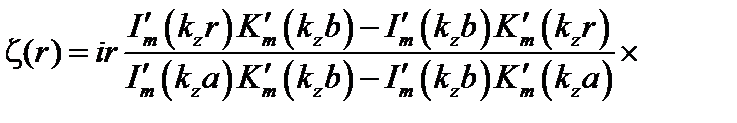
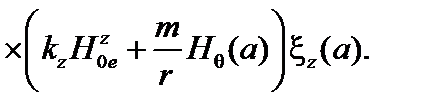 (3.5.10)
(3.5.10)
В пределе 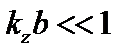 выражение (3.5.10) упрощается:
выражение (3.5.10) упрощается:
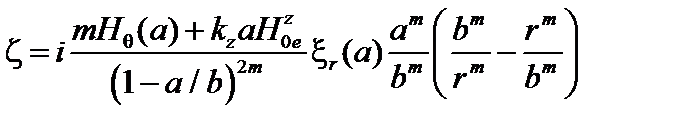 , (3.5.11)
, (3.5.11)
а функционал, отнесённый к единице длины системы, принимает вид
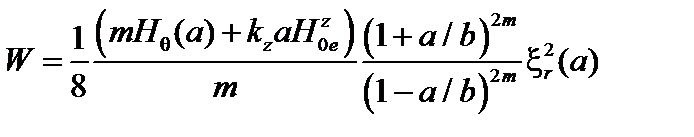 . (3.5.12)
. (3.5.12)
Пусть в цилиндре с отождествлёнными концами на одном периоде укладывается 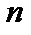 периодов возмущения. Тогда
периодов возмущения. Тогда 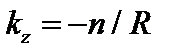 , и
, и
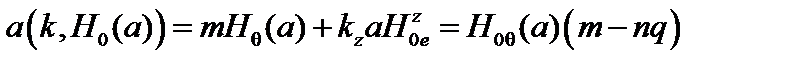 . (3.5.13)
. (3.5.13)
В результате получаем функционал в следующем виде:
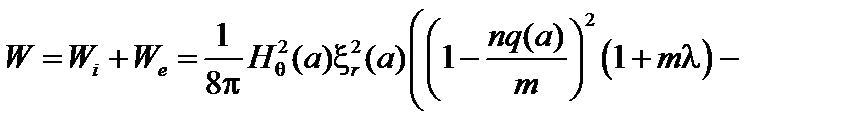
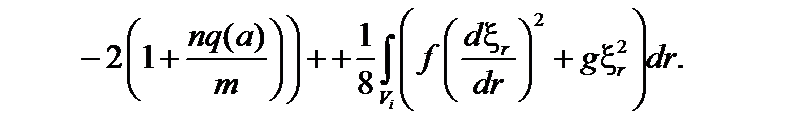 (3.5.14)
(3.5.14)
Здесь
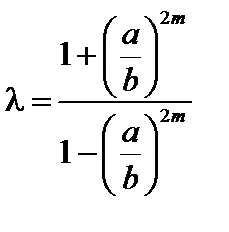 ;
;
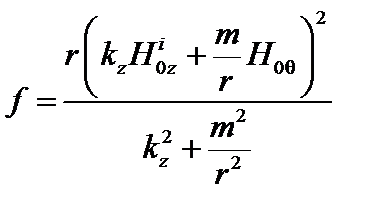 ;
; 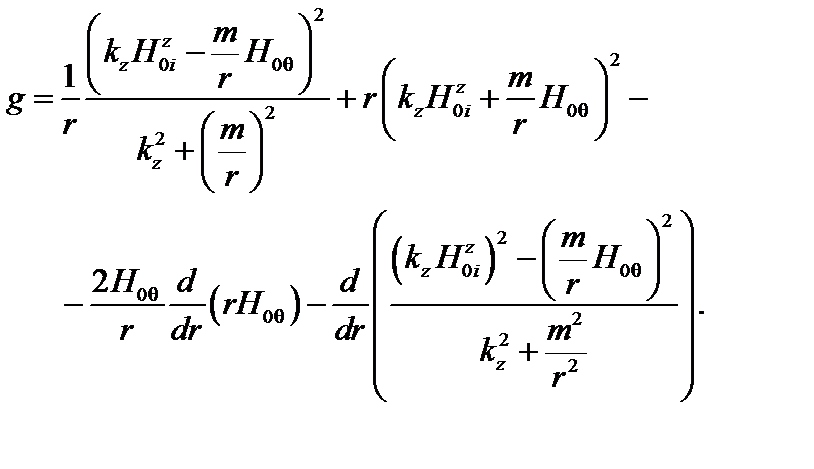
Первый член в правой части (3.5.14) отрицателен, если 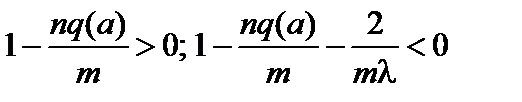 , или
, или
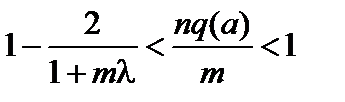 . (3.5.15)
. (3.5.15)
Учитывая (3.5.2), функцию 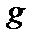 можно переписать так:
можно переписать так:
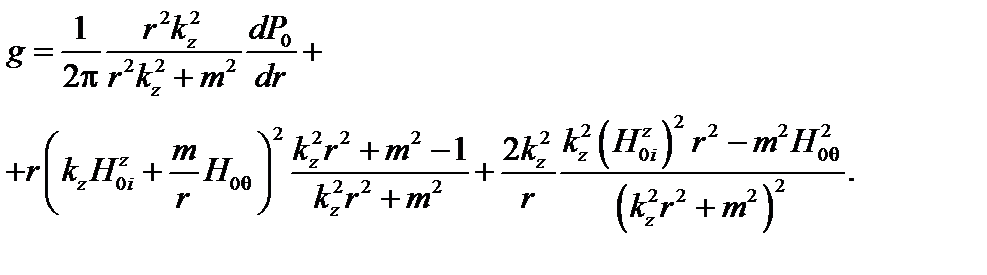
Оценим теперь вклад в 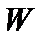 последнего (интегрального) члена. Пусть
последнего (интегрального) члена. Пусть 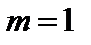 . Тогда обе функции
. Тогда обе функции 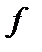 и
и 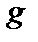 имеют порядок
имеют порядок 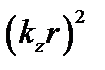 , и последним членом в (3.5.14) можно пренебречь. В этом случае величина
, и последним членом в (3.5.14) можно пренебречь. В этом случае величина 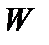 становится отрицательной, если
становится отрицательной, если
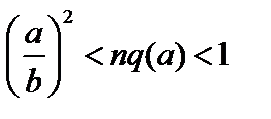 , (3.5.16)
, (3.5.16)
и любое начальное возмущение нарастает. Скорость нарастания возмущения можно оценить, используя уравнение (2.2.3). В фурье-представлении 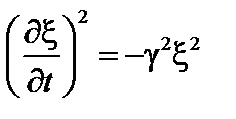 , где
, где 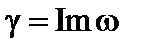 – инкремент неустойчивости. С помощью (2.3.3) получаем
– инкремент неустойчивости. С помощью (2.3.3) получаем
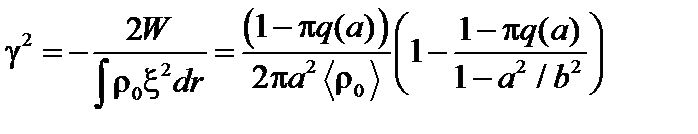 . (3.5.17)
. (3.5.17)
Здесь 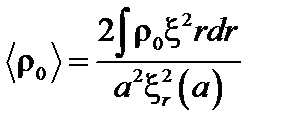 .
.
Максимальную величину инкремента по порядку величины можно оценить так:
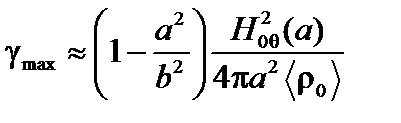 . (3.5.18)
. (3.5.18)
Легко видеть, что этот инкремент по порядку величины равен отношению альфвеновской скорости к радиусу плазмы и может составлять в токамаке по порядку величины 10-8 с, то есть развитие такой неустойчивости является одним из наиболее быстрых процессов.
Пусть теперь 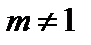 . Тогда функция
. Тогда функция 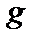 может быть порядка единицы в некоторой области значений
может быть порядка единицы в некоторой области значений 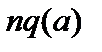 :
:
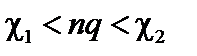 , (3.5.19)
, (3.5.19)
где 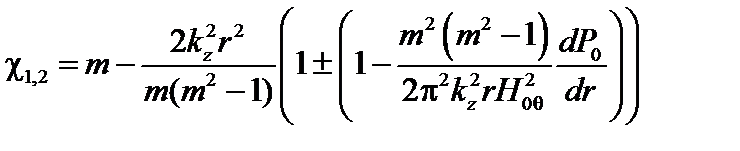 .
.
Зависимость 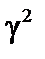 от
от 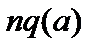 качественно представлена на рис. 10.
качественно представлена на рис. 10.
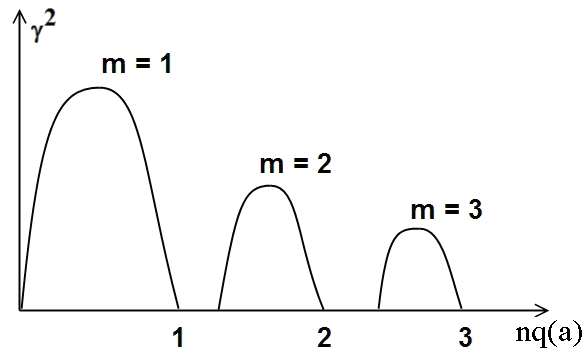
Рис. 10. Качественная зависимость квадрата инкремента от 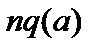
для различных мод
Как видно, области неустойчивости чередуются с областями устойчивости, где 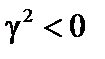 . Именно в этих областях и работает токамак.
. Именно в этих областях и работает токамак.
 2015-08-21
2015-08-21 585
585








