2015-08-21
713
Более общим случаем возмущений цилиндрической плазменной конфигурации является винтовое возмущение. Идеальную винтовую моду в иностранной литературе называют «kink mode». Будем в этом разделе следовать монографии [3].
Для анализа таких возмущений вернемся к достаточно общему уравнению (2.1.31). Напомним, что это уравнение описывает идеальную плазму, то есть плазму с бесконечной проводимостью. Как и в предыдущем разделе, градиент давления и ток в плазме (за исключением тока по поверхности) равны нулю. Такое распределение тока имеет место в пинчах:
(3.3.1)
Будем рассматривать несжимаемую плазму
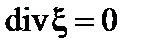. (3.3.2)
Тогда уравнение (2.1.31) существенно упрощается:
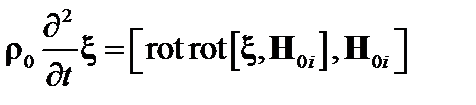. (3.3.3)
Ищем решение этого уравнения в виде
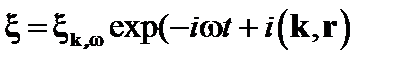. (3.3.4)
Так как смещение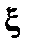 
зависит от радиуса-вектора, волновой вектор является оператором,
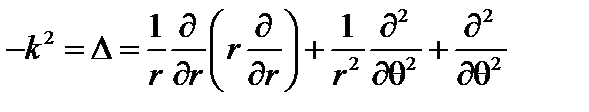. (3.3.5)
Подставляя это выражение в (3.3.2) и учитывая, что 
, окончательно получаем
. (3.3.6)
Умножим это уравнение скалярно на 
. В силу (3.3.2) левая часть полученного равенства обращается в ноль. Правая часть обращается в ноль, если
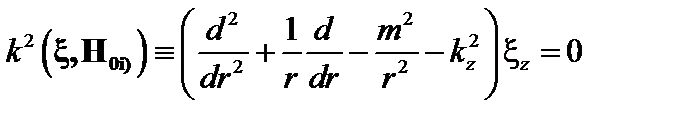. (3.3.7)
Мы предположили, что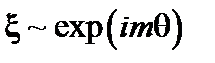 
, где m – целое число.
Общим решением уравнения (3.3.7) является линейная комбинация модифицированной функции Бесселя и функции Кельвина:
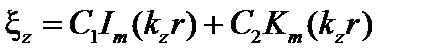, (3.3.8)
где С1 и С2 – произвольные постоянные. Функция Km расходится в нуле, поэтому С1 = 0. Выражая C2 через 
, имеем
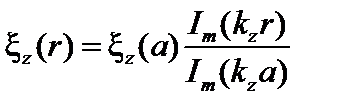. (3.3.9)
Подставим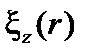 
в радиальную компоненту уравнения (3.3.6), имея в виду, что радиальная составляющая волнового вектора является оператором, 
.
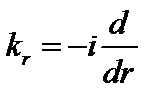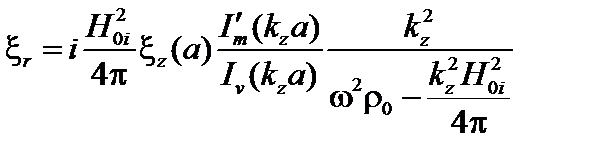. (3.3.10)[1]
Штрих означает производную по аргументу. Это решение должно быть «сшито» с решением в вакуумной области, где rot H = 0. Следовательно, магнитное поле может быть представлено как градиент некоторой функции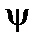 
. Тогда уравнение div H = 0переходит в уравнение Лапласа, решение которого снова имеет вид (3.3.8). Но во внешней области 
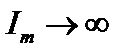при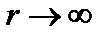 
, поэтому С1 = 0. В результате
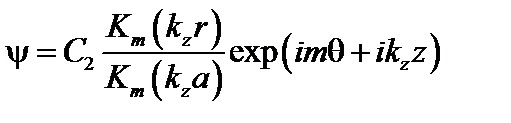. (3.3.11)
На границе плазмы должно выполняться условие (2.1.38). При условии несжимаемости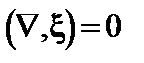 
оно приводится к виду
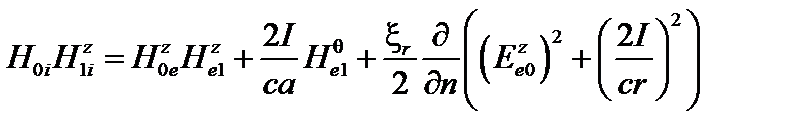. (3.3.12)
Из (2.1.27) находим
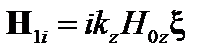, (3.3.13)
а для возмущения поля во внешней области
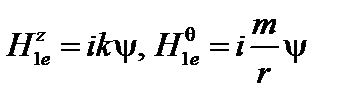. (3.3.14)
Подставляем эти выражения в (3.3.12):
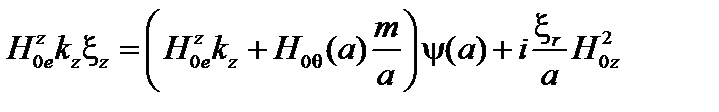. (3.3.15)
Еще одно краевое условие – это обращение в ноль на границе тангенциальной составляющей электрического поля в системе отсчета, движущейся вместе с плазмой,
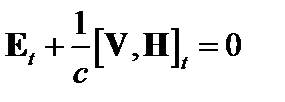. (3.3.16)
Берем rot от этого уравнения, учитываем, что в линейном приближении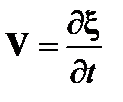 
, и используем нормальную к границе составляющую уравнения Максвелла 
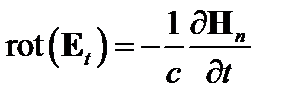. В результате получаем
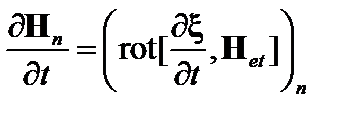. (3.3.17)
Интегрируем это уравнение по времени:
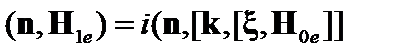. (3.3.18)
Учитывая, что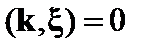 
, это равенство можно переписать следующим образом:
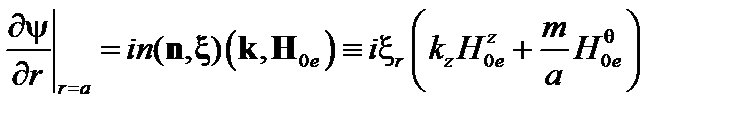. (3.3.19)
Продифференцируем по радиусу (3.3.11) и подставим в левую часть этого равенства. Отсюда находим
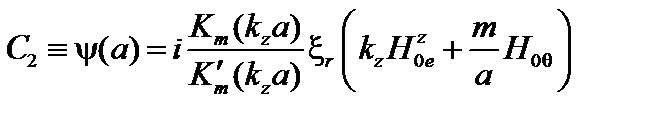. (3.3.20)
Подставляя (3.3.10) и (3.3.20) в (3.3.15), получаем в результате дисперсионное уравнение
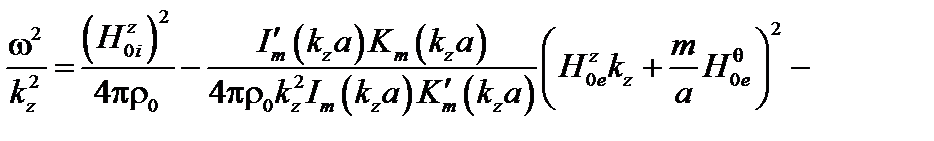
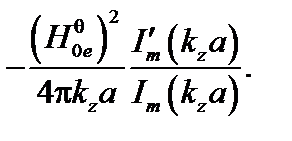(3.3.21)
Неравенство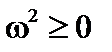 
является критерием устойчивости системы. Поскольку 
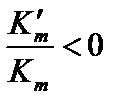, второй член в правой части (так же, как и первый) – стабилизирующий. Он имеет минимум, если множитель 
.
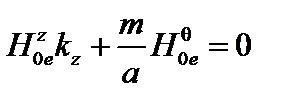Пусть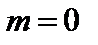 
, 
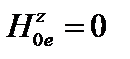. Условие устойчивости (3.3.21) упрощается:
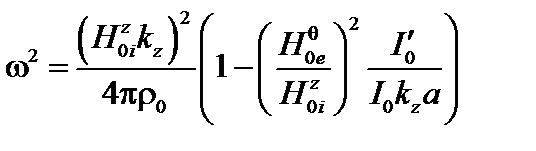. (3.3.22)
Так как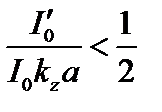 
, мода заведомо устойчива, если 
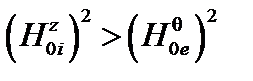. Этот случай соответствует перетяжкам и уже был рассмотрен в разделе 3.2.
Мода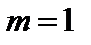 
, 
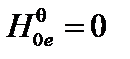– это винтовая мода, «змейки» в русскоязычной литературе или «kink-mode» в англоязычной. Рассмотрим эту моду в пределе длинных волн, 
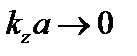. При этом для цилиндрических функций можно использовать разложение в ряд:
; 
.
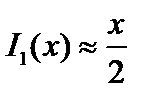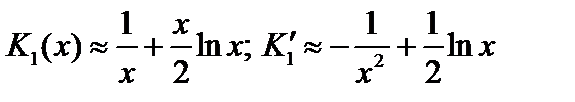При этом дисперсионное уравнение (3.3.21) принимает вид
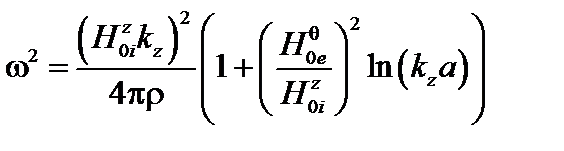. (3.3.23)
В рассмотренном случае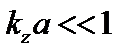 
второй член в скобках отрицателен, и плазма может быть неустойчивой.
Рассмотрим типичный для токамака случай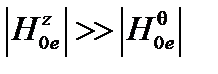 
. Снова будем исследовать предел 
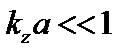. Разложим в ряд функции Бесселя и Кельвина:
;
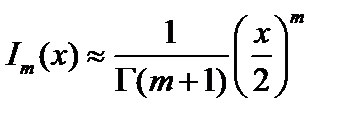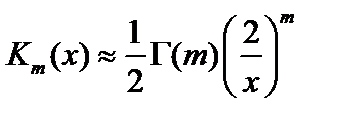для 
.
Здесь 
; 
.
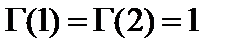Дисперсионное уравнение (3.3.21) в этом приближении имеет вид
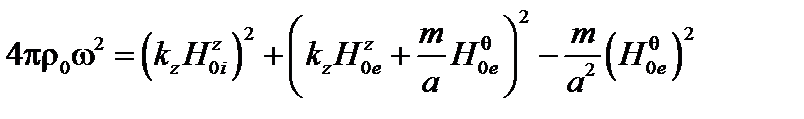. (3.3.24)
Квадрат частоты является квадратичной формой волнового вектора 
(рис. 9).
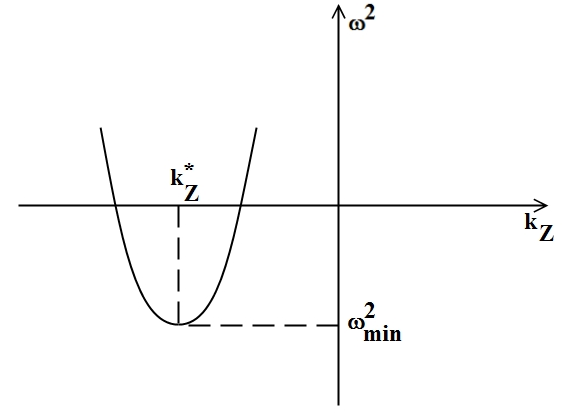
Рис. 9. Качественная зависимость квадрата частоты от kz
Значение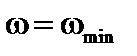 
, соответствующее минимуму этой кривой, определяет максимальный инкремент. Это достигается при значении 
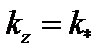, когда парабола достигает минимума, т. е.
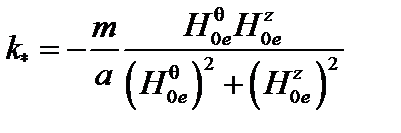. (3.3.25)
Условие устойчивости имеет вид
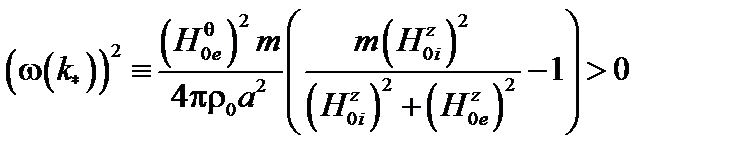. (3.3.26)
Выразим это условие устойчивости через параметр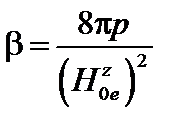 
.
Условие равновесия при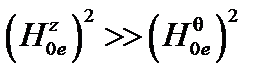 
принимает вид 
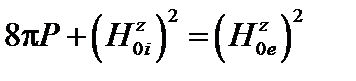, что можно переписать так:
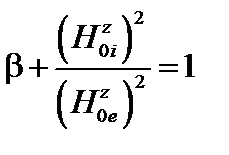. (3.3.27)
Выражая правую часть неравенства (3.3.26) через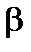 
, получаем условие устойчивости
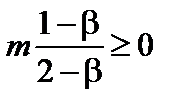, (3.3.28)
что в пределе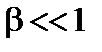 
дает
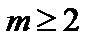. (3.3.29)
Это означает, что моды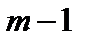 
и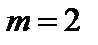 
неустойчивы, остальные – устойчивы.
В реальных тороидальных системах величина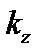 
ограничена снизу, 
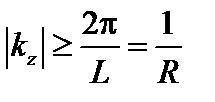, где 
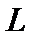и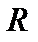 
– длина окружности и большой радиус тороидальной системы.
В бесконечном цилиндре наиболее неустойчива мода с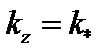 
. В случае цилиндра с отождествленными концами на 
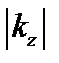налагается ограничение 
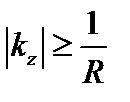, и если 
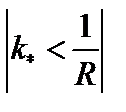, то наиболее неустойчивой оказывается мода с 
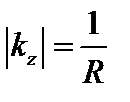. Для этого случая при 
, 
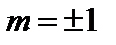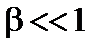условие (3.3.24) можно переписать как
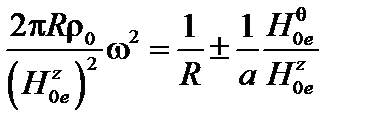. (3.3.30)
Плазма устойчива, если положительна правая часть этого равенства,
.
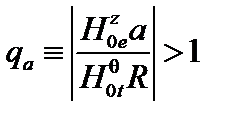Это условие называют условием Крускала–Шафранова, а величину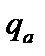 
– коэффициентом запаса устойчивости Шафранова.
Данное условие несколько модифицируется, если плазменный цилиндр окружён бесконечно проводящей стенкой при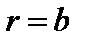 
. В этом случае дисперсионное уравнение превращается в следующее:
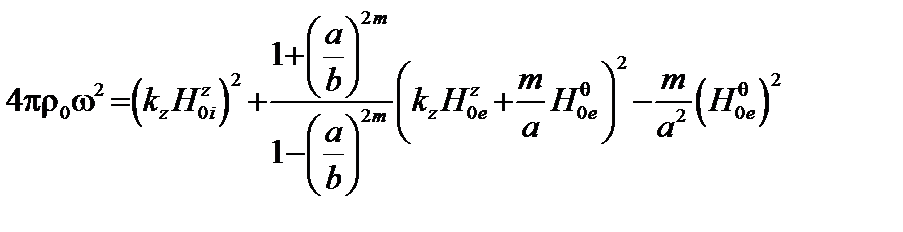. (3.3.31)
При удалении бесконечно проводящей стенки на бесконечность дисперсионное уравнение переходит в уравнение (3.3.24). При приближении стенки к границе плазмы система становится устойчивой.
