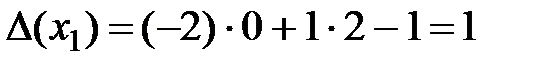
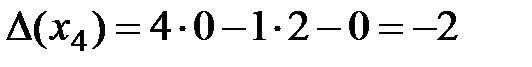
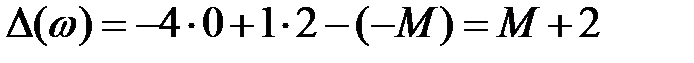
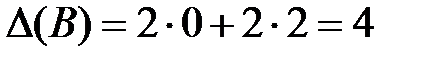 .
.
| 
| -М | 
| 
| ||||
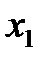
| 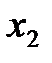
| 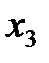
| 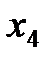
| 
| ||||
| 10:4=2,5 | |||||||
| -М | -1 | 2:1=2-min | |||||

| -М | -М | М | -2М | ||||
| -1 | -2 | |||||||
| -2 | .4. | -4 | 2: 4 = 1/2 | ||||
| -1 | |||||||

| М | |||||||
| -2 | ||||||||
| -1/2 | 1/4 | -1 | 1/2 | ||||
| 1/2 | 1/4 | 5/2 | 5/2: 1/2= 5 | ||||

| М | |||||||
| 1/2 |
Так как все индексные оценки неотрицательны, то найдено оптимальное решение задачи. При этом все свободные переменные (отсутствующие в столбце 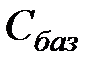 последней симплекс таблицы) равны 0. Базисные переменные
последней симплекс таблицы) равны 0. Базисные переменные 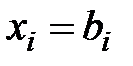 . Значение целевой функции равно
. Значение целевой функции равно 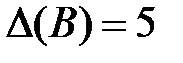 .
.
То есть, 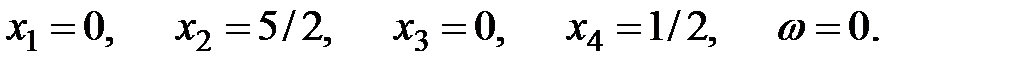 Так как
Так как 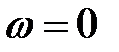 , то получено и решение первоначальной задачи
, то получено и решение первоначальной задачи 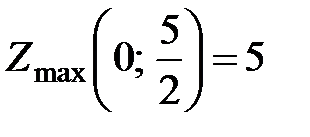 . Оптимальный план
. Оптимальный план 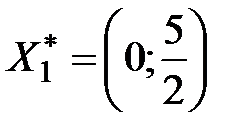 . Проверим, является ли он единственным.
. Проверим, является ли он единственным.
В случае единственного решения число нулевых индексных оценок должно равняться числу базисных переменных. В данном случае число базисных переменных (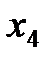 и
и 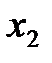 ) равно 2, а нулевых индексных оценок три:
) равно 2, а нулевых индексных оценок три: 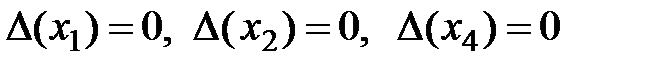 . Следовательно, задача имеет бесконечное множество решений. Т.к. одна свободная переменная имеет нулевую индексную оценку, то существует еще одно оптимальное решение, линейно независимое с полученным решением. Вводя
. Следовательно, задача имеет бесконечное множество решений. Т.к. одна свободная переменная имеет нулевую индексную оценку, то существует еще одно оптимальное решение, линейно независимое с полученным решением. Вводя 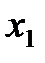 (свободную переменную с нулевой индексной оценкой) в базис, перейдем к следующей симплекс таблице. Т.е. разрешающий столбец
(свободную переменную с нулевой индексной оценкой) в базис, перейдем к следующей симплекс таблице. Т.е. разрешающий столбец 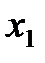 . В нем только один положительный элемент 1/2, который является разрешающим. Симплекс таблица приобретет следующий вид.
. В нем только один положительный элемент 1/2, который является разрешающим. Симплекс таблица приобретет следующий вид.
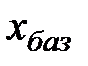
| 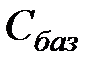
| -М | 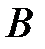
| 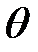
| ||||
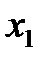
| 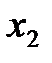
| 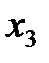
| 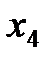
| 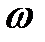
| ||||
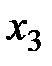
| 10:4=2,5 | |||||||
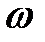
| -М | -1 | 2:1=2-min | |||||

| -М | -М | М | -2М | ||||
| -1 | -2 | |||||||
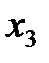
| -2 | .4. | -4 | 2: 4 = 1/2 | ||||
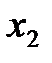
| -1 | |||||||

| М | |||||||
| -2 | ||||||||
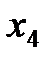
| -1/2 | 1/4 | -1 | 1/2 | ||||
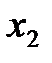
| 1/2 | 1/4 | 5/2 | 5/2: 1/2= 5 | ||||

| М | |||||||
| 1/2 | ||||||||
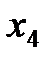
| 1/2 | -1 | ||||||
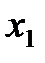
| 1/2 | |||||||

| М | |||||||
| 1/2 |
Выпишем полученное решение М-задачи 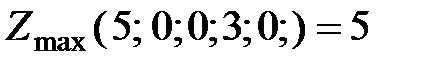 и решение первоначальной задачи
и решение первоначальной задачи 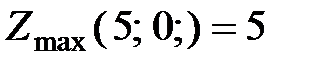 . Оптимальный план
. Оптимальный план 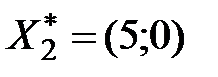 .
.
Итак, максимальное значение 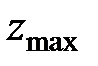 достигается в двух вершинах многоугольника, а, следовательно, и на отрезке прямой соединяющей эти вершины (на стороне многоугольника). Общий оптимальный план (любая точка этой стороны многоугольника) имеет вид:
достигается в двух вершинах многоугольника, а, следовательно, и на отрезке прямой соединяющей эти вершины (на стороне многоугольника). Общий оптимальный план (любая точка этой стороны многоугольника) имеет вид: 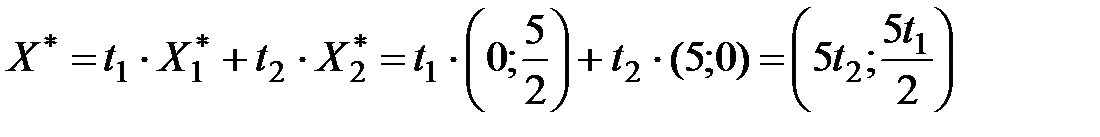 , где
, где 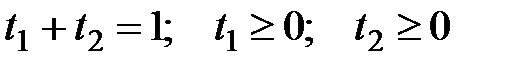 .
.
Если обозначить 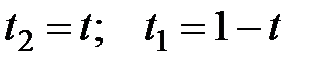 , то ответ можно записать так: задача имеет бесконечное множество решений.
, то ответ можно записать так: задача имеет бесконечное множество решений.
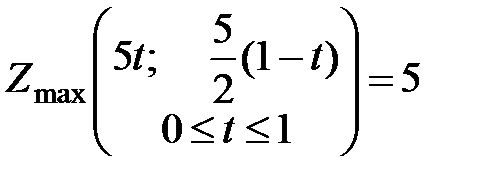 .
.
Пример
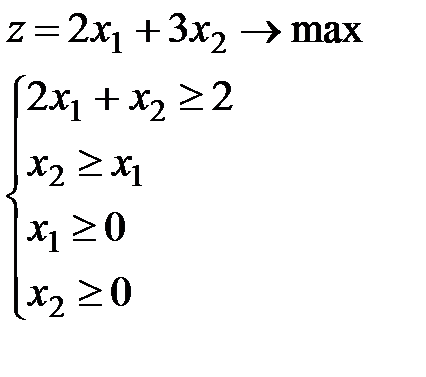
 2015-08-21
2015-08-21 306
306








