Основная концепция метода конечных элементов

Главная трудность при непосредственном применении классических методов взвешенных невязок связана с выбором базисных функций для области определения в целом. Эти функции должны не только удовлетворять граничным условиям, но и достаточно полно описывать геометрию и другие характеристики задачи. Все эти условия обычно трудно выполнить, особенно для объектов (конструкций) сложной геометрии при наличии сложного теплообмена, и поэтому возможности методов в их классическом смысле весьма ограничены.

С появлением быстродействующих ЭВМ получила развитие идея локализации аппроксимирующих функций в малых областях (подобластях), называемых конечными элементами [2, 3, 4, 6].

Пусть имеется некоторая область определения задачи, ограниченная контуром 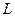, как это изображено на рис. 2.1. Внутри этой области и на ее контуре можно задать произвольное количество точек с координатами 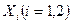. Значения искомой функции в этих точках пусть будут 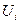. Соединяя точки прямыми линиями, получим подобласти, совокупность которых аппроксимирует область в целом. При этом криволи-

нейные участки контура L заменяется прямолинейными. Важно отметить, что полученная сетка из элементов, с помощью которой моделируется область определения за-

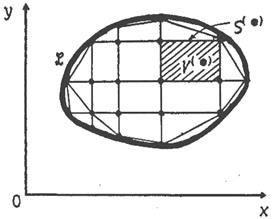дачи, не является регулярной ни Рис. 2.1 Разбиение области на элемент ы

геометрически, ни топологически. Это означает, что размеры и формы подобластей

(элементов) могут изменяться произвольно, их взаимные соединения не обязательно должны следовать какой-либо регулярной структуре. Последнее обстоятельство обеспечивает геометрическую гибкость метода.

Важной особенностью МКЭ является то, что первоначально при локальной аппроксимации функции на конечных элементах, их можно рассматривать независимо друг от друга. Это значит, что каждый элемент можно считать изолированным от всей совокупности и аппроксимировать функцию на этом элементе с помощью ее значений в его узлах независимо от того, какое место займет рассматриваемый элемент в связанной модели, и от поведения функции на других конечных элементах. С математической точки зрения это означает следующее. Для каждого элемента записывается локальная (элементная) аппроксимирующая функция:

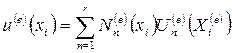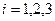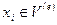, , , (2.2.1.)

где 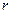− число узлов, принадлежащих 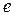- му элементу; 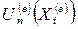− значения искомой функции в его узлах; 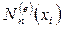− базисная функция; 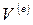− объем элемента.

Поскольку каждый элемент рассматривается отдельно, то его свойства изучаются независимо от других элементов, т.е. дифференциальное уравнение с соответствующими граничными условиями решается для каждого 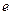- го элемента, например, методом Галеркина [2, 3, 4, 12]:

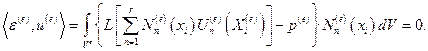(2.2.2)

Полученные на основании (2.2.2) матрицы для отдельных элементов, которые содержат в качестве неизвестной узловые значения функции 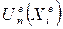, формируют в глобальные матрицы для всей области определения. Разрешая полученную таким образом систему алгебраических уравнений, определяют значения искомой функции в узлах, что позволяет найти приближенное решение задачи для всей области в целом:

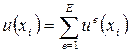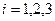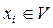, , , (2.2.3)

где 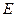– число элементов, совокупность которых аппроксимирует область 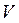в целом.

Реализация в рамках МКЭ представления области определения совокупностью конечных элементов обусловливает следующие важные преимущества МКЭ, обеспечивая его широкое применение для решения задач теории поля:

• локальная аппроксимация на каждом элементе единственным образом опре-

деляется значениями искомой функции в узловых точках;

• обеспечивается широкая вариация задания граничных условий на отдельных

участках границы (внешней и внутренней) области;

• криволинейные участки границ области могут быть аппроксимированы пря-

мыми линиями;

• размеры и геометрическая форма элементов могут быть разными;

• взаимные соединения элементов не обязательно должны следовать какой-

либо регулярной структуре;

• свойства материала каждого элемента могут быть индивидуальными и, к тому

же, анизотропными;

• обеспечивается возможность повышения точности решения задачи путем уве-