Краевые условия задачи

В задачах теории поля единственность решения уравнения переноса (1.1.14) обеспечивается заданием краевых условий задачи: начального поля искомой величины в момент времени, выбранный за нулевой :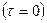

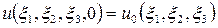, (1.2.1)

и граничных условий, которые в задачах теории поля чаще всего формулируются в виде следующих условий на границе (или ее части) области определения задачи:

а) задано поле температур 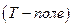−так называемое главное граничное условие:
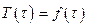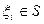, ; (1.2.2)

б) задано обобщенное условие сложного теплообмена [1] − или естественное граничное условие:

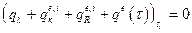, (1.2.3)

входящие в (1.2.3) слагаемые описывают теплообмен: 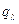- кондуктивный; 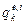-конвективный (на внешних 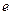и внутренних 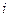поверхностях элемента); 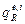− радиационный (внешний и внутренний); 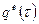− внешний поверхностный источник тепла, зависящий в общем случае от времени. Поверхность 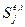представляет собой 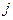- й участок внешней или внутренней границ, и в совокупности образует oбe границы области в целом (в случае ее многосвязности).

В задачах теплопроводности принято граничные условия задачи подразделять на четыре рода, а именно:

1-го рода – Т(х_i,τ) = f(х_i), при этом функция может быть задана в виде константы, например, Т(х_i,τ) = Т_с;

2-го рода – (q_λ + q_c)_Si = 0; где q_c – внешний поверхностный источник энергии (Вт/м²), чаще всего равный константе; кондуктивный компонент описывается законом Фурье;

3-го рода – (q_λ + q_α)_Si = 0; связывает кондуктивный и конвективный удельные потоки на поверхности S_i; конвективный компонент описывается законом Ньютона;

4-го рода – полагаются непрерывными температурные поля и удельные тепловые потоки на границе раздела двух сред: Т_i(x_i)_Sk = T_j(x_j)_Sk; q_λi(x_i)_Sk = q_λj(x_j)_Sk.

По определению граничное условие – это условие энергетического сопряжения на внешней поверхности тела при наличии двух (трех) механизмов теплообмена или на границе раздела двух сред. По сути – это условия теплового баланса на поверхности раздела.

Кондуктивный компонент описывается законом Фурье и в обобщенной криволинейной системе координат согласно (1.1.5) имеет вид:

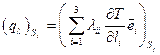. (1.2.4)

Конвективный компонент в аналитической теории теплопроводности обычно выражают законом Ньютона [20]:

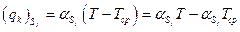, (1.2.5)

где 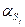– коэффициент теплообмена при естественной или смешанной конвекциях, вопросам расчета которого посвящена обширная литература [19–29], но в аналитической теории теплопроводности он полагается заданным в виде некоторого числа; Т_ср.– температура среды или теплоносителя.

Радиационный компонент нелинейно зависит от температуры и, согласно закону Стефана-Больцмана [30]:

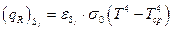, (1.2.6)

где 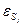− полусферическая интегральная степень черноты поверхности; 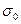= 5,67·10^-8 Вт/м²К⁴ – постоянная Стефана-Больцмана.

Запишем естественное граничное условие (1.2.3) с учетом (1.2.4)−(1.2.6) в обобщенном виде:

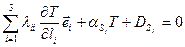, (1.2.7)

где под 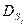понимается величина:

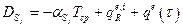. (1.2.8)

В целях линеаризации граничного условия радиационный компонент зачастую представляют в виде, аналогичном конвективному компоненту [20, 24, 32]:

,

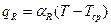где 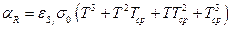, и затем объединяют с конвективным компонентом, вводя суммарный коэффициент теплообмена 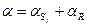. Величину 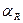рассчитывают, полагая 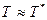− некоторой характерной температуре изучаемого процесса [32]. Если при описании внешнего радиационного теплообмена с такой процедурой линеаризации можно согласиться, то для внутреннего теплообмена подобная замена нежелательна, так как в этом случае радиационный компонент рассчитывается с учетом оптико-геометрического фактора – средних разрешающих угловых коэффициентах излучения, обусловленного взаимным расположением теплообменивающихся поверхностей и их степеней черноты.

1.3* Краткая характеристика методов решения краевой задачи

Классификация методов решения тесно связана с видом математической

формулировки задачи теплопроводности. Кроме того, их можно разделить по общим

признакам на три большие группы: точные аналитические, приближенные аналити- ческие и численные методы.

Аналитические методы позволяют получить функциональные зависимости для распределения температуры и проанализировать влияние различных факторов на тем-

пературное поле исследуемого объекта [20 –24]. Для математической формулировки задачи в виде дифференциального уравнения теплопроводности и соответствующих краевых условий определение температурного состояния тела связано с непосредственным решением этого уравнения. Возможности точных аналитических методов в этом случае ограничены, как правило, решением линейных задач теплопроводности, когда теплофизические характеристики материала не зависят от температуры, а граничные условия выражается линейной комбинацией температуры и ее градиента на поверхности тела. Сферу применения точных аналитических методов удается расширить путем линеаризации нелинейных задач. Однако при этом погрешности, внесенные в математическую формулировку при линеаризации, в некоторых случаях могут быть настолько существенными, что приведут к большим количественным ошибкам, а иногда исказят и физический смысл полученного решения [44].

Точное аналитическое решение нелинейных задач теплопроводности обычно возможно лишь при определенных сочетаниях зависимостей теплофизических характеристик материала тела от температуры [26]. Возможности точных аналитических методов в случае анизотропности теплофизических свойств крайне ограничены. Наконец, эти методы приложимы к получению и исследованию температурного поля тел (конструкций) простой геометрической формы (пластина, цилиндр, шар) и лишь при осесимметричных граничных условиях. Тем самым, задание локальных граничных условий, наиболее часто встречающихся в реальных конструкциях, из рассмотрения исключается.

_________________________________________________________________________

٭ Этот пункт может быть опущен читателем, знакомым с методами решения краевых задач, без ущерба для понима­ния последующего материала.

Для приближенного аналитического решения нелинейных дифференциальных уравнений теплопроводности разработаны методы последовательных приближений (простой итерации [24] или усреднения функциональных поправок [24]), возмущений (малого параметра), различные асимптотические и вариационные методы [20, 24].

Инженерные методы расчета температурных полей конструкций (или их элементов) сочетают в себе как приближенные аналитические, так и численные методы [19, 31, 36, 44, 52].

Методы численного решения являются приближенными, так как они базируются на переходе от непрерывной (континуальной) математической модели процесса теплопроводности к приближенной дискретной модели. Однако выбор параметров дискретной модели позволяет регулировать степень приближения, а гибкость и универсальность численных методов в сочетании с удобством их реализации на ЭВМ дает возможность получать приемлемые для инженерной практики результаты.

С точки зрения достоверности определения температур элементов конструкции и возможностей учета влияния всех существенных факторов, наиболее эффективными являются численные методы. Совершенствование и распространение вычислительной техники превращают эти методы в удобный, а, зачастую, и единственный инструмент анализа тепловых режимов конструкций и агрегатов различного назначения на стадиях их проектирования и экспериментальной отработки [31, 38, 47, 48, 50– 52].

Численные методы базируются, как правило, на уравнении переноса, представленном в дифференциальной или в интегральной формах. Различия между ними состоят в способе использования уравнения и краевых условий. Одними из широко распространенных являются методы, основанные на конечно-разностной аппроксимации уравнения и граничных условий. Однако по точности они уступают численным методам решения нелинейных интегральных уравнений [24].

При решении тепловых задач комплексного проектирования объектов космической техники широко используется так называемый метод изотермических элементов (метод алгебраического приближения), основанный на системе уравнений элементарного баланса тепловых потоков в дискретной модели конструкции, состоящей из теплоемких масс и теплопроводящих стержней (элементов) [32, 45 – 52]. Достоинство метода – исключительная геометрическая гибкость; недостаток – сложность расчета кондуктивных связей между элементами и, главное, отсутствие полной физической адекватности исследуемому процессу переноса (игнорирование контактного термического сопротивления на границе между элементами).

Задание 1

1.1 Получите выражения уравнения переноса (1.1.14) в декартовой,

цилиндрической и сферической системах координат – S = 1,2,3.

1.2 Проделайте эту же операцию для граничных условий (1.2.7).