Методы взвешенных невязок

Большая группа методов приближенного решения дифференциальных

уравнений базируется на математической формулировке, связанной с

интегральным представлением взвешенной невязки. Эту группу методов называют методами взвешенных невязок [4, 12, 13].

Пусть имеется дифференциальное уравнение и граничное условие к нему:

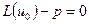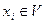, , (2.1.1)

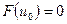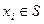, . (2.1.2)

Здесь L −дифференциальный оператор; x_i − пространственные координаты; V и S − объем и внешняя граница исследуемой области; u₀ – точное решение.

Будем считать, что некоторая функция u также является решением уравнения, и оно может быть аппроксимировано набором функций :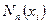

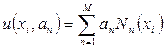, (2.1.3)

при этом коэффициенты 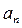− неизвестные величины, подлежащие определению с помощью некоторой математической процедуры.

В методах невязки эта процедура состоит из двух последовательных этапов. На первом этапе подстановкой приближенного решения (2.1.3) в уравнение (2.1.1) находится функция 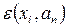ошибка, или невязка, которая характеризует степень отличия 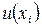от точного решения :

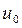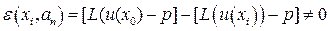. (2.1.4)

В итоге получается алгебраическое уравнение, содержащее текущие координаты 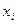и М по-прежнему неизвестных коэффициентов .

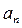На втором этапе на функцию невязки (2.1.4) накладываются требования, которые минимизируют или саму невязку (метод коллокаций), или взвешенную невязку (метод наименьших квадратов и метод Галеркина).

В методе коллокаций полагают, что дифференциальное уравнение удовлетворяется только в некоторых выбранных (произвольно) точках − точках коллокаций 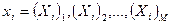, количество которых равно числу неизвестных коэффициентов 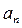. В этих М точках невязка должна равняться нулю, что приводит к системе М алгебраических уравнений для М коэффициентов :

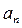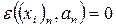. (2.1.5)

В методах взвешенной невязки сначала формируют взвешенную невязку путем ее умножения на некоторые весовые функции 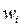, а затем минимизируют ее в среднем:

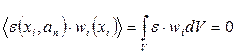. (2.1.6)

В методе наименьших квадратов − методе Рэлея-Ритца − в качестве весовой функции выбирается сама ошибка, т.е. 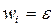, и требуется, чтобы полученная таким способом величина (функционал) была минимальна:

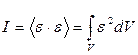. (2.1.7)

Для этого должно выполняться условие:

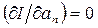, (2.1.8)

приводящее к системе алгебраических уравнений относительно неизвестных коэффициентов.

В методе Галеркина в качестве весовых функций берутся сами функции 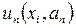, называемые базисными, и требуется их ортогональность невязке :

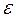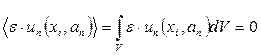. (2.1.9)

Если 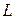− линейный оператор, то система (2.1.9) переходит в систему алгебраических уравнений относительно коэффициентов .

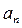Рассмотрим метод Галеркина на конкретном примере [4]. Дано уравнение на промежутке :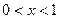

,

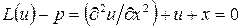с граничными условиями: , .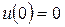

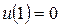Возьмем аппроксимирующую функцию в следующем виде:

,

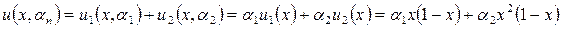удовлетворяющей граничным условиям (2.1.2) при любых 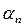. На первом этапе находим невязку:

.

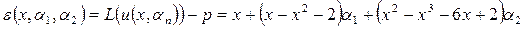Выполним процедуру второго этапа:

, .

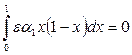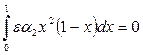Интегрирование приведет к системе двух уравнений:

,

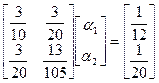решением которых будут следующие значения 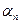: 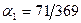; 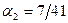. Приближенное решение имеет вид: .

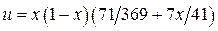Сопоставление приближенных результатов, полученных различными методами, с точным решением дано в таблице 1.

Таблица 1

x	u приближенное	u точное
метод кол- локаций	метод Ритца	метод Галеркина
0,25	0,045	0,043	0,0440	0,044014
0,50	0,071	0,068	0,0698	0,069747
0,75	0,062	0,059	0,0600	0,060056

Из таблицы 1 видно, что при одинаковых во всех методах аппроксимирующих функциях наилучшее приближение к точному решению обеспечивает метод Галеркина. Кроме того, этот метод применим при решении и нелинейных задач, включая те, для которых не существует функционала, необходимого при использовании метода Рэлея-Ритца.