| S | ∂/∂li | dV | ||
| i=1 | i=2 | i=3 | ||
| ∂/∂x ∂/∂ r ∂/∂ r | ∂/∂y (1/ r) ∂/∂θ (1/rSinβ) ∂/∂θ | ∂/∂z ∂/∂z (1/r) ∂/∂β | dxdydz rdrdθdz r2drdθSinβdβ |
ричных 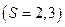 элементов. У полностью симметричных элементов оно сократится до двух – вследствие азимутальной симметрии
элементов. У полностью симметричных элементов оно сократится до двух – вследствие азимутальной симметрии 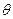 - й компонент
- й компонент 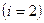 исчезнет.
исчезнет.
Вторую матрицу в (5.1.5), также умножаемую на вектор-столбец 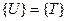 , по аналогии называют матрицей теплопроводности элемента, но ее поверхностной частью (интегрирование ведется по поверхности
, по аналогии называют матрицей теплопроводности элемента, но ее поверхностной частью (интегрирование ведется по поверхности 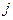 - ой грани):
- ой грани):
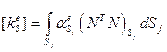 ,
, 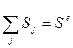 . (5.2.3)
. (5.2.3)
Нижний индекс 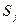 у матричного произведения базисных функций означает, что базисные функции узлов, не принадлежащих
у матричного произведения базисных функций означает, что базисные функции узлов, не принадлежащих 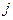 - й поверхности, должны быть заменены нулями согласно их свойству (4.5.1), а объемные (трехмерные) базисные функции принадлежащих грани узлов – преобразованы, т.е. из объемных превращены в двумерные поверхностные базисные функции, так как поверхность описывается уравнением
- й поверхности, должны быть заменены нулями согласно их свойству (4.5.1), а объемные (трехмерные) базисные функции принадлежащих грани узлов – преобразованы, т.е. из объемных превращены в двумерные поверхностные базисные функции, так как поверхность описывается уравнением 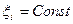 (т.е. нормальна орту
(т.е. нормальна орту 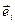 ). Очевидно, что и
). Очевидно, что и 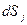 для разных поверхностей выражается по-разному.
для разных поверхностей выражается по-разному.
Проиллюстрируем сказанное на конкретном примере. Пусть 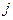 - й поверхностью является нижняя грань второго элемента каталога и ей присвоен номер 1. Она содержит узлы
- й поверхностью является нижняя грань второго элемента каталога и ей присвоен номер 1. Она содержит узлы 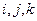 , и, следовательно, базисные функции остальных узлов
, и, следовательно, базисные функции остальных узлов 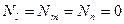 . Уравнение плоскости, которой принадлежит первая поверхность:
. Уравнение плоскости, которой принадлежит первая поверхность: 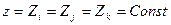 . Это означает, что в базисных функциях узлов этой поверхности текущую переменную
. Это означает, что в базисных функциях узлов этой поверхности текущую переменную 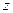 нужно заменить на их
нужно заменить на их 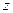 - e координаты, в силу чего на основании (4.3.3) полином Лагранжа
- e координаты, в силу чего на основании (4.3.3) полином Лагранжа 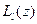 станет равным единице. Для базисной функции на этой грани будем иметь:
станет равным единице. Для базисной функции на этой грани будем иметь:
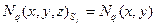 ,
, 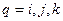 ,
, 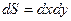 .
.
Вторая – верхняя грань – идентична первой, но у нее 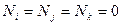 ,
,
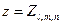 , поэтому
, поэтому 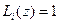 .
.
Остальные грани не являются в общем случае координатными плоскостями, и поэтому базисные функции их узлов нельзя преобразовать; кроме того, 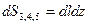 , что усложняет процедуру интегрирования. Число компонент объемной части матрицы теплопроводности (5.2.1) равно трем.
, что усложняет процедуру интегрирования. Число компонент объемной части матрицы теплопроводности (5.2.1) равно трем.
Базисные функции тетраэдра также, очевидно, не преобазуются в общем случае, но процедура интегрирования упрощается переходом к естественной системе координат (см. п. 5.3).
В матричном представлении второй член в решении (5.1.5) имеет вид,
аналогичный (5.2.2):
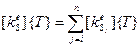 , (5.2.4)
, (5.2.4)
где 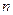 - число граней элемента, на которых
- число граней элемента, на которых 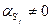 .
.
Число компонент поверхностной части матрицы теплопроводности в общем случае равно числу n граней элемента, т.е. n = 4÷6. Для удобства математического представления матрицы (5.1.2) и (5.1.4) объединяют (их ранги одинаковы), что дает:

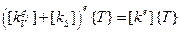 , (5.2.5)
, (5.2.5)
где 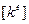 – матрица теплопроводности элемента (матрица жесткости в задачах упругости).
– матрица теплопроводности элемента (матрица жесткости в задачах упругости).
Третий член выражения (5.1.5) принято называть матрицей демпфирования в задачах упругости, и матрицей теплоемкости в задачах теплопроводности:
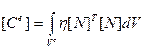 . (5.2.6)
. (5.2.6)
Как видно из (5.2.6), матрица [ 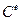 ] всегда симметрична; η = cp ρ = Cv– объемная теплоемкость материала элемента.
] всегда симметрична; η = cp ρ = Cv– объемная теплоемкость материала элемента.
Физический смысл этой матрицы в обеих задачах один и тот же, – она демпфирует (уменьшает) изменения определяемой величины( в частности, температуры) и, тем самым, характеризует инерционные свойства материала элемента (следовательно, и объекта в целом).
Остальные члены, именуемые объемной и поверхностной частями вектора тепловой нагрузки (вектор нагрузки в задачах упругости), запишутся так:
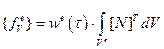 ; (5.2.7)
; (5.2.7)
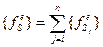 ; где
; где 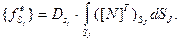 (5.2.8)
(5.2.8)
Процедура нахождения поверхностных частей матрицы теплопроводности (5.2.3) и вектора тепловой нагрузки (5.2.8) идентичны. Число компонент поверхностной части вектора тепловой нагрузки равно количеству граней элемента, на которых 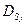 ≠ 0. В общем случае число компонент равно 4÷6.
≠ 0. В общем случае число компонент равно 4÷6.
Для удобства записи оба вектора объединяют в один вектор тепловой нагрузки:
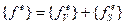 .
.
Собирая все члены, получим определяющую элемент систему 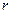 (по числу
(по числу
узлов элемента) обыкновенных дифференциальных уравнений первого порядка в их матричном представлении:

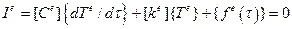 . (5.2.9)
. (5.2.9)
Переход от частной производной по времени к обыкновенной объясняется тем, что временная производная рассматривается как функция только координат в каждый фиксированный момент времени. Стационарный случай 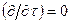 будет описываться системой
будет описываться системой 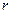 алгебраических уравнений:
алгебраических уравнений:
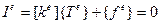 . (5.2.10)
. (5.2.10)
 2015-08-21
2015-08-21 349
349








