2015-08-21
256
Из курса матричной алгебры известно, что произведение матрицы размером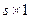 
(вектор-столбец) на матрицу размером 
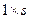(матричная строка) дает матрицу размером 
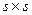. Поэтому подынтегральные выражения в формуле (5.1.5) для вклада элемента с r узлами в решение задачи представляют собой матрицы размером r x r, или – как последние два члена – вектор-столбцы размером 
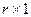. Так как интегралы берутся в определенных размерами элемента пределах, членами проинтегрированных матриц будут – в конечном итоге – числа, независимо от того, в каком виде удается осуществить интегрирование – в аналитическом или в численном.
Каждая матрица имеет свое традиционное наименование в зависимости от физической природы решаемой задачи. Так, в задачах теплопроводности первый член в (5.1.5) называют объемной частью (интегрирование ведется по объему элемента) матрицы теплопроводности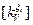 
, описываемой выражением
(5.2.1):
.
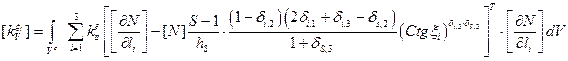Верхний индекс показывает, по какой переменной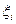 
осуществляется дифференцирование базисных функций элемента. Ранг матрицы равен 
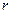, где 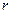–число узлов элемента. У элементов базового каталога r = 4÷8.
Вид производных базисных функций, полученный на основании (1.1.13) –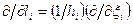 
– с учетом значений параметров Ляме в различных системах координат (см. (1.1.10)), представлен в таблице 3.
В матричном представлении первый член в (5.1.5) имеет вид:
, 
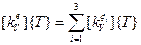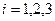. (5.2.2)
В соответствии с физической природой задачи вместо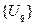 
берем температуру 
.
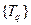Число компонент объемной части матрицы теплопроводности (5.2.1) равно
трем (по числу координат) для естественно ограниченных (S=1) ограниченно симмет-
Таблица 3
