2015-08-21
254
Хвилі, що описуються гармонійною функцією, називаються
гармонійними хвилями. Рівняння плоскої гармонійної хвилі, що розповсюджується в позитивному напрямі осі x, прийнято записувати у вигляді:
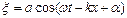. (8.1)
Введемо визначення: величину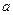 
називають амплітудою хвилі, 
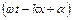- фаза хвилі, 
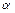- початкова фаза; вона визначається вибором початку відліку координати x і часу t. Величина 
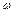є циклічна (кругова) частота коливань частинок середовища. З періодичності функції 
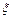за часом знаходимо 
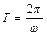- період коливань частинок.
Коефіцієнт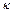 
називають хвильовим числом. Його можна представити як 
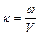, де v – швидкість поширення хвилі.
Відстань, на яку поширюється хвиля за час, що дорівнює періоду коливань частинок, називається довжиною хвилі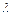 
:
.
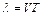Довжина хвилі пов'язана з хвильовим числом співвідношенням:
.
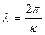Фазовою швидкістю хвилі називається швидкість переміщення в просторі поверхні постійної фази хвилі. З умови сталості фази для гармонійної плоскої хвилі (8.1) маємо
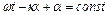. (8.2)
Це рівняння є рівнянням площини у просторі. Швидкість її переміщення і є фазовою швидкістю хвилі:
.
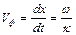Зазначимо, що у разі гармонійної хвилі фазова швидкість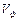 
збігається зі швидкістю хвилі, тобто зі швидкістю поширення коливань частинок середовища.
Хвильовим вектором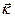 
називають вектор, який визначається виразом:
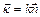
або
,
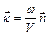де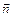 
- одиничний вектор, перпендикулярний до хвильової поверхні.
