Оценки характеристик генеральной совокупности

Первичная обработка выборки.

Эмпирическая функция распределения 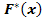генеральной совокупности.

Оценки характеристик генеральной совокупности.

1. По дискретной выборке:

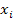
	-2

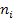
1) найти 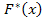, построить полигон частот, полигон относительных частот;

2) вычислить точечные оценки математического ожидания, дисперсии, СКО;

3) найти моду, медиану и коэффициент вариации.

2. По интервальной выборке признака х:

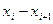
	2-4	4-6	6-8	8-10	10-12

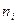
1) построить гистограмму частот, гистограмму относительных частот, 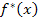, выдвинуть гипотезу о законе распределения;

2) перейти к дискретному ряду, найти и построить 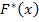, полигон частот, полигон относительных частот;

3) найти точечные оценки .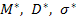

4) найти интервальные оценки с надежностью 0,95 математического ожидания и дисперсии.

Д/з.:

3. По дискретной выборке:

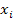
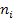
1) найти 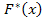, построить полигон частот, полигон относительных частот;

2) вычислить точечные оценки математического ожидания, дисперсии, СКО;

3) интервальные оценки этих числовых характеристик с надежностью 0,95;

4) найти моду, медиану и коэффициент вариации.

4. Построить гистограмму частот и гистограмму относительных частот по данному интервальному распределению выборки объема 100.

Номер интервала	Интервал	Частота
	[1;5]
	(5;9]
	(9;13]
	(13;17]
	(17;21]

1) предполагая, что признак Х –НСВ, построить схематически график эмпирической плотности распределения вероятностей ;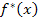

2) предполагая, что признак Х –НСВ и выбрав в качестве вариант 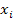– середину i -го интервала, составить эмпирическую функцию распределения ;

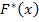3) найти точечные и интервальные оценки 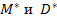с доверительной вероятностью ;

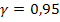4) найти медиану и коэффициент вариации.