Непрерывной называют случайную величину, которая может принимать бесконечное, несчетное число значений (т.е. ее значения заполняют конечный или бесконечный промежуток (a, b) числовой прямой).
Функция распределения для НСВ Х определяется так же, как и для ДСВ: 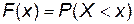 . Но, в отличие от ДСВ, функция распределения НСВ непрерывна на всей числовой прямой.
. Но, в отличие от ДСВ, функция распределения НСВ непрерывна на всей числовой прямой.
Свойства функции распределения были приведены в предыдущем пункте. Они справедливы и для ДСВ, и для НСВ.
Но для НСВ при нахождении вероятности попадания Х в интервал не важно, включены ли в интервал его концы:
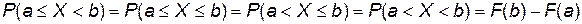 .
.
При этом для НСВ невозможно принять какое-либо конкретное значение, т.е. 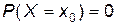 .
.
Плотностью распределения (дифференциальной функцией) непрерывной случайной величины называется функция 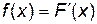 .
.
Кривой распределения называется график плотности распределения.
Свойства плотности распределения:
1) 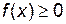 .
.
2) 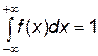 . (Графически это означает, что площадь под кривой распределения равна 1)
. (Графически это означает, что площадь под кривой распределения равна 1)
3) 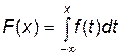 .
.
4) 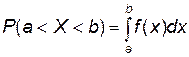 .
.
 2015-09-07
2015-09-07 253
253








