Если число испытаний n велико, а вероятности p и q не очень близки к нулю, то вероятность 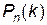 можно рассчитать по локальной формуле Муавра-Лапласа:
можно рассчитать по локальной формуле Муавра-Лапласа: 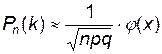 , где
, где 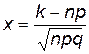 ,
, 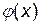 – функция Гаусса, значения которой можно определить по Приложению 1.
– функция Гаусса, значения которой можно определить по Приложению 1.
Свойства функции 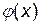 :
:
а) 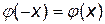 (функция четная); б) если
(функция четная); б) если 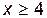 , то
, то 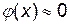 .
.
Интегральная формула Муавра-Лапласа
Если число испытаний n велико, а вероятности p и q не очень близки к нулю, то вероятность 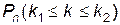 того, что число успехов заключено между
того, что число успехов заключено между 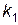 и
и 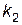 , можно рассчитать по интегральной формуле Муавра-Лапласа:
, можно рассчитать по интегральной формуле Муавра-Лапласа: 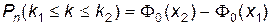 , где
, где 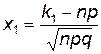 ,
, 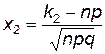 ,
,
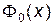 – функция Лапласа (ее значения можно найти в Приложении 2).
– функция Лапласа (ее значения можно найти в Приложении 2).
Свойства функции 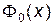 :
:
а) 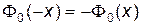 (функция нечетная); б) если
(функция нечетная); б) если 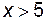 , то
, то 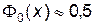 .
.
 2015-09-07
2015-09-07 343
343








