| Гипотеза H 0
| Условие
| Статистика
| Пояснения
| |
| Для нормальных генеральных совокупностей
| |
D (X) = D (Y) или
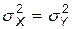
|
| Fнабл = 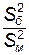 (распределение Фишера)
(распределение Фишера)
| 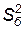 – б о льшая, а – б о льшая, а
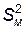 – меньшая исправленные дисперсии. – меньшая исправленные дисперсии.
| |
| |
| M (X)= M (Y)
| Генеральные дисперсии известны:
D (X) и D (Y)
| 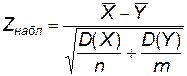 (нормальное распределение) (нормальное распределение)
| 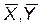 –выборочные средние, –выборочные средние,
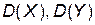 – известные генеральные дисперсии,
n, m – объемы выборок X, Y – известные генеральные дисперсии,
n, m – объемы выборок X, Y
| |
| |
| |
| Генеральные дисперсии неизвестны, но одинаковы:
D (X)= D (Y)
| 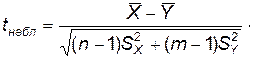 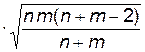 (распределение Стьюдента)
(распределение Стьюдента)
| 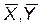 –выборочные средние, –выборочные средние,
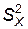 , , 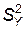 – выборочные исправленные дисперсии,
n, m – объемы выборок X, Y. – выборочные исправленные дисперсии,
n, m – объемы выборок X, Y.
| |
| |
| |
| Генеральные дисперсии неизвестны и неодинаковы
| 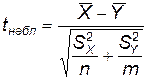 (распределение Стьюдента)
(распределение Стьюдента)
| 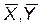 – выборочные средние, – выборочные средние,
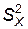 , , 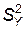 – выборочные исправленные дисперсии,
n, m – объемы выборок X, Y. – выборочные исправленные дисперсии,
n, m – объемы выборок X, Y.
| |
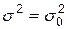
|
| 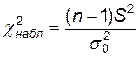 (
(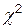 –распределение) –распределение)
| S 2 – исправленная выборочная дисперсия.
| |
| Гипотеза H 0
| Условие
| Статистика
| Пояснения
| |
| Для нормальных генеральных совокупностей
| |
| а = a 0
| Генеральная дисперсия известна:
D (X) = s 2
| 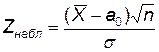 (нормальное распределение)
(нормальное распределение)
| 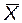 – выборочное среднее,
n – объём выборки, – выборочное среднее,
n – объём выборки,
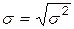 – известное среднее квадратическое отклонение – известное среднее квадратическое отклонение
| |
| |
| |
| Генеральная дисперсия неизвестна
| 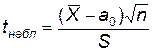 (распределение Стьюдента)
(распределение Стьюдента)
| 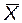 – выборочное среднее,
n – объём выборки, – выборочное среднее,
n – объём выборки, 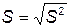 , где S 2 – исправленная выборочная дисперсия. , где S 2 – исправленная выборочная дисперсия.
| |
| |
| |
| Для биномиальных выборок
|
|
| p 1 = p 2
|
| 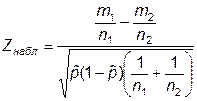 (нормальное распределение)
(нормальное распределение)
| n 1, n 2 – количества испытаний, m 1, m 2 – числа появлений в них "успеха".
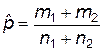
| |
| |
| |
| p = p 0
|
| 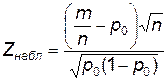 (нормальное распределение)
(нормальное распределение)
| n – число испытаний,
m – число "успехов".
| |
| |
| |
| Проверка гипотезы о значимости выборочного коэффициента корреляции
| |
| r Г = 0
|
| 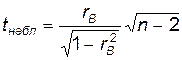 (распределение Стьюдента
(распределение Стьюдента
| rВ – выборочный коэффициент корреляции,
n – объем выборки.
| |
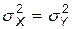
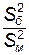 (распределение Фишера)
(распределение Фишера)
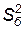 – б о льшая, а
– б о льшая, а
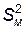 – меньшая исправленные дисперсии.
– меньшая исправленные дисперсии.
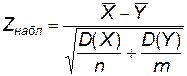 (нормальное распределение)
(нормальное распределение)
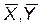 –выборочные средние,
–выборочные средние,
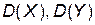 – известные генеральные дисперсии,
n, m – объемы выборок X, Y
– известные генеральные дисперсии,
n, m – объемы выборок X, Y
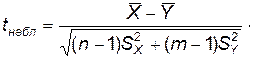
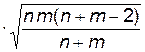 (распределение Стьюдента)
(распределение Стьюдента)
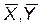 –выборочные средние,
–выборочные средние,
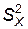 ,
, 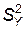 – выборочные исправленные дисперсии,
n, m – объемы выборок X, Y.
– выборочные исправленные дисперсии,
n, m – объемы выборок X, Y.
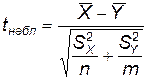 (распределение Стьюдента)
(распределение Стьюдента)
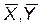 – выборочные средние,
– выборочные средние,
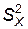 ,
, 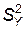 – выборочные исправленные дисперсии,
n, m – объемы выборок X, Y.
– выборочные исправленные дисперсии,
n, m – объемы выборок X, Y.
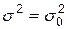
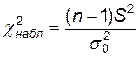 (
(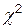 –распределение)
–распределение)
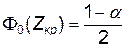
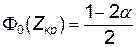
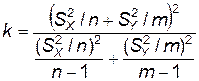
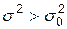
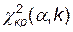
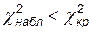
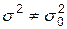
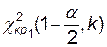 ,
, 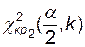
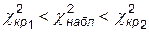
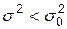
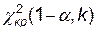
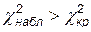
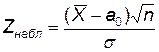 (нормальное распределение)
(нормальное распределение)
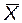 – выборочное среднее,
n – объём выборки,
– выборочное среднее,
n – объём выборки,
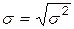 – известное среднее квадратическое отклонение
– известное среднее квадратическое отклонение
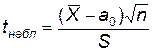 (распределение Стьюдента)
(распределение Стьюдента)
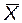 – выборочное среднее,
n – объём выборки,
– выборочное среднее,
n – объём выборки, 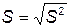 , где S 2 – исправленная выборочная дисперсия.
, где S 2 – исправленная выборочная дисперсия.
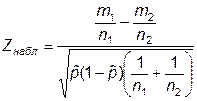 (нормальное распределение)
(нормальное распределение)
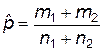
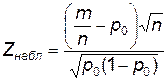 (нормальное распределение)
(нормальное распределение)
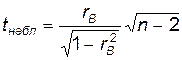 (распределение Стьюдента
(распределение Стьюдента
 2015-09-07
2015-09-07 262
262







