2015-09-07
229
Статистический ряд распределения имеет вид:
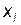
| x 1 | x 2 | … | xk | S |
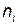
| n 1 | n 2 | … | nk | n |
Относительная частота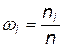 
, где n – объем выборки.
Накопленная относительная частота: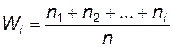 
.
Полигон частот [ относительных частот ] – ломаная, соединяющая точки с координатами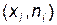 
[ 
].
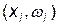Гистограмма относительных частот – фигура, состоящая из прямоугольников. Основания прямоугольников – это частичные интервалы, а высота i -го прямоугольника определяется формулой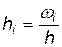 
, где h – длина частичного интервала.
Гистограмма – это аналог кривой распределения НСВ.
Кумулята – ломаная, соединяющая точки с координатами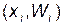 
.
Кумулята – статистический аналог графика функции распределения.
Для непрерывного признака строится интервальный ряд распределения.
Число интервалов определяется по формуле Стерджеса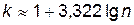 
.
Длина интервала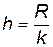 
(округляется в б о льшую сторону), где 
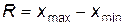– размах варьирования (вариации).
Эмпирической функцией распределения называется функция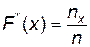 
, где nx – число вариант, меньших х; n – объем выборки.
