Лекция 13
Фрактальные алгоритмы
Геометрические фракталы
Геометрическими названы фракталы, форма которых может быть описана как последовательность простых геометрических операций. Геометрические фракталы строятся на основе исходной фигуры – линии, полигона, полиэдра – путем ее дробления и выполнения аффинных и логических преобразований (объединения или исключения) полученных фрагментов.
Метод построения фрактального объекта может быть как итерационным, так и рекурсивным, причем рекурсивный чаще бывает богаче возможностями и проще в программировании.
Вообще алгоритм построения кривой Кох можно применить к любому многоугольнику или ломаной линии, запустив алгоритм построения кривой Кох для каждого из составляющих фигуру отрезков (в приложении 2 содержится программа построения кривой Кох и фрактального треугольника с помощью этой процедуры).
Алгоритмические фракталы
Фрактал Мандельброта. Мандельброт исследовал предельное (при k ® ¥) поведение последовательности комплексных чисел zk+ 1 = zk 2 + z 0, k= 0, 1, 2, …; z 0 =c при различных значениях комплексных чисел c.
Последовательность zk с ростом числа итераций демонстрирует поведение двух типов в зависимости от выбора начальной точки z 0. Ее элементы либо постепенно уходят в бесконечность, либо всегда остаются в определенной замкнутой области, совершая циклическое движение или сходясь в точку.
Математиками строго доказано, что если при некотором k модуль | zk|>r min, где r min=2 – минимальный радиус расходимости множества Мандельброта, то далее последовательность расходится.
Множество точек z 0, для которых последовательность не расходится, называется множеством Мандельброта.
Графическая интерпретация множества Мандельброта удивительно красива и бесконечно разнообразна. Для ее получения используется следующий алгоритм. Комплексное число z=x+iy может быть изображено на плоскости точкой с координатами
(x, y). Изображение строится в некоторой прямоугольной области с разрешением n * m точек.
Формула итераций для фрактала Мандельброта выглядит следующим образом:
zk+ 1 = zk 2 + z 0, k= 0, 1, 2, …
Цикл итераций для фрактала Мандельброта можно выполнять в диапазоне для x 0 = (от -2,2 до 1), для y 0=(от -1,2 до 1,2) – начальные точки z 0.
Для каждой начальной точки вычисляется количество k точек, попадающих в круг сходимости (k – число итераций). Условием завершения итераций является |zk|> 2.
Суть алгоритма сводится к итерационному выводу точек, попадающих в круг сходимости для каждой начальной точки, в пределах заданного графического окна. Для каждого цикла итерации (для каждой начальной точки) выбирается свой цвет.
Если принять значения k для каждой начальной точки (x, y) в качестве высот некоторой поверхности в данной точке можно построить объемное изображение множества Мандельброта или его части, которое при специально подобранном освещении может выглядеть и как скала с плоской вершиной, и как водопад, и как горная пещера.
Типичный фрактал, каким является множество Мандельброта, представляет собой иерархический объект, состоящий из родительского тела в форме кардиоиды и многочисленных потомков, повторяющих форму предков, от которых они ответвляются. Само подобие элементов фрактала хорошо видно на его изображении.
Связность множества означает, что его элементы, даже самого малого размера, которые Мандельброт назвал "фрактальной пылью", не обособлены, а соединены тончайшими нитями в одно целое. Продолжая процесс увеличения пограничных областей, мы всюду видим бесконечное разнообразие форм, поражающих гармонией, великолепием и удивительным сходством с изображениями регулярно-хаотических явлений природы: молний, снежинок, ледяного узора, инея на ветвях деревьев, кораллов, паутины, солнечных протуберанцев, звездных скоплений и т.п.
Фрактал Джулио (Жюлио) внешне совсем не похож на фрактал Мандельброта, хотя формула итераций для этого фрактала почти полностью совпадает с формулой для фрактала Мандельброта:
zk+ 1 = zk 2 + c, k= 0, 1, 2, …
где c – комплексная константа.
Если при генерации фрактала Мандельброта значение z 0 каждый раз совпадает со значением в начальной точке на данном шаге итераций, то для фрактала Джулио значение c всегда одно и то же комплексное число.
В программе, (приведенной в приложении 2), построено изображение фрактала Джулио для c= 0,36+ i* 0,36.
Итерационная формула для фрактала Ньютон имеет вид
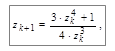
где z – также комплексные числа, причем z 0 =x+iy соответствует координатам точки изображения. Условием прекращения цикла итераций для фрактала Ньютон есть приближение значений |z 4-1| к нулю.
Границы расчета: для x – от -1 до 1, для y – от -1 до 1.
 2015-09-07
2015-09-07 692
692







