Некоторые общие положения регрессионного анализа

Регрессионный анализ (РА) - метод математической статистики, который позволяет выявить приближенную количественную зависимость (f) свойства объекта y от значений факторов x _j, оказывающих влияние на это свойство. Эта приближенная зависимость, выраженная в виде конкретной математической функции, называется уравнением регрессии:

.

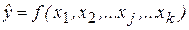Проводить РА можно только для количественных значений y и x _j.

При РА решают две основные задачи:

1. Ищут с помощью метода приближения уравнение регрессии, наиболее точно описывающее истинную зависимость y = j(x _j) по результатам измерения свойств объекта при различных значениях факторов:

y = j(x ₁, x ₂,..., x _j,... x _k) + e = f(x ₁, x ₂,..., x _j,... x _k) + q + e.

2. Оценивают ошибки (q + e), допускаемые при описании истинной зависимости j с помощью найденного уравнения регрессии.

Порядок проведения РА (его тип) зависит от плана эксперимента. Различают классический РА (КРА) и РА при математическом планировании эксперимента (РАМПЭ).

5.3.2. Составление планов эксперимента для проведения регрессионного анализа

5.3.2.1. Составление планов эксперимента для проведения классического регрессионного анализа

Общим требованием к планированию любого эксперимента для проведения КРА является выполнение условия m_j > 2. Другие рекомендации аналогичны планированию эксперимента для проведения дисперсионного анализа.

После планирования и завершения эксперимента проведение КРА его результатов проводят в такой последовательности:

Выбирают семейство математических функций, в котором предполагается найти уравнение регрессии (семейство прямых, парабол, гипербол и др.).

Выбирают метод приближения.

Для выбранного семейства функций с помощью метода приближения рассчитывают параметры функции (коэффициенты уравнения регрессии).

Проверяют рассчитанные коэффициенты уравнения регрессии на значимость (равенство нулю).

Корректируют вид исходной функции, исключая из нее незначимые коэффициенты и другие составляющие.

Рассчитывают параметры скорректированной функции (скоррек­тированные коэффициенты уравнения регрессии) и возвращаются к выполнению пунктов 4,5. Пункт 6 выполняют до тех пор, пока в уравнении регрессии останутся только значимые коэффициенты (значения коэффициентов могут изменяться после каждого пересчета)

Оценивают ошибки (q + e), допускаемые при описании истинной зависимости j с помощью найденного уравнения регрессии: проверяют адекватность уравнения регрессии с помощью закона распределения Фишера или рассчитывают вероятность описания зависимости j функцией f.

Выбирают другое семейство математических функций и (или) метод приближения и с ними последовательно выполняют пункты 3-7.

Из группы найденных уравнений регрессии в ряду разных семейств функций выбирают окончательное уравнение регрессии по следующим соображениям:

а) вид данного уравнения регрессии совпадает с теоретическими законами поведения объекта;

б) данное уравнение регрессии описывает поведение объекта с наибольшей вероятностью;

в) при одной вероятности для данного уравнения регрессии наблюдается наибольшее значение соотношения факторной и остаточной дисперсий (F-соотношения).

При выборе семейства функций (пункты 1 и 8), если нет сведений или теоретических предположений о типе зависимости j, обычно действуют по принципу "от простого к сложному". При этом начинают с семейства прямых ("линейная регрессия") или трансцендентных функций, которые легко преобразуются в линейную форму ("трансцендентная регрессия").

При неадекватности найденного линейного уравнения регрессии или неудовлетворенности его точностью можно переходить к семейству полиномов с постепенным увеличением их степени (полиномы второго, третьего и др. порядков) до тех пор, пока не начнет уменьшаться F-соот­ношение. Вид функции также зависит от числа одновременно изменяемых факторов при эксперименте.

Наиболее часто при выполнении РА в качестве метода приближения используют метод наименьших квадратов (МНК). Однако применение МНК является корректным при выполнении следующих требований:

а) единичные результаты измерения свойств y должны быть независимыми случайными величинами;

б) выборочные дисперсии y _z должны быть однородными (одинаковыми).

При невыполнении этих условий используют другие методы приближения (непараметрические методы регрессии).

Алгоритмы всех необходимых при КРА расчетов (пункты 3,4,6,7) зависят от выбранного семейства функций, метода приближения, наличия повторных опытов, количества исследуемых факторов (изучить самостоятельно [6,7,8,11]). Многие из этих алгоритмов реализованы в статистических программных продуктах, математических пакетах (MathCAD и др.), электронных таблицах (E x cel и др.).

Следует отметить, что выполнение пункта 9 носит субъективный характер и для него пока еще нет общепризнанных рекомендаций.

Пример проведения классического регрессионного анализа. Воспользуемся для примера данными эксперимента, приведенными в
табл. 7.

По полю корреляции (см. рис. 4) можно предположить линейный характер зависимости y от х, поэтому начнем проведение КРА с выбора семейства прямых и представления искомого уравнения регрессии в виде

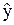= а + b x.

Так как в этом эксперименте не проводились повторные опыты, то невозможно оценить однородность дисперсий при различных уровнях фактора х и установить закон распределения y. Поэтому делаем допущение о нормальном законе распределения y и равенстве дисперсий (одинаковой случайной ошибке при любом значении х). Тогда в качестве метода приближения можно взять МНК.

Используя метод МНК и учитывая отсутствие повторных опытов, выполним расчеты коэффициентов уравнения регрессии а и b [1]:

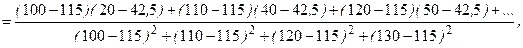
b = 1,3 (мас. %/мин); a = ` y - b` x = 42,5 - 1,3×115;

а = - 107 (мас. %).

Так как дисперсия воспроизводимости эксперимента 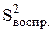неизвестна и ее невозможно определить (из-за отсутствия повторных опытов), то проверку коэффициентов а и b на значимость не проводим. Делаем допущение, что эти коэффициенты "значимы", т.е. не равны нулю.

Найденное линейное уравнение регрессии имеет следующий вид:

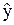= - 107 + 1,3 х.

Для оценки ошибки, допускаемой при описании истинной зависимости j с помощью найденного уравнения регрессии при отсутствии повторных опытов и дисперсии воспроизводимости, составим F-соотно­шение (F_p) между дисперсией относительно` y (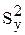) и остаточной дисперсией (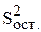) в соответствии со следующими формулами:

; ; ,

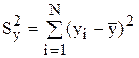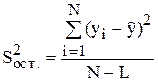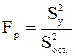где L - число значимых коэффициентов в скорректированном уравнении регрессии (L = 2).

Выполним необходимые расчеты:

,

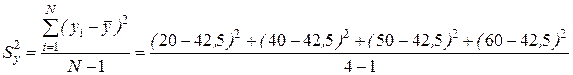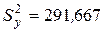» 290 (мас. %)²;

,

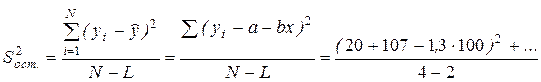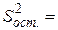15 (мас. %)²;

;

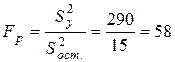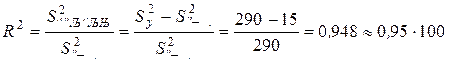% = 95 %;

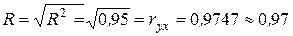(где R - выборочный корреляционный коэффициент Пирсона, R² - коэффициент детерминации).

Найденное линейное уравнение регрессии (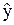 = - 107 + 1,3 х) с вероятностью, большей 0,95, адекватно описывает реальную зависимость выхода нитробензола от времени его синтеза, так как значение соотношения F_p больше табличного значения квантиля распределения Фишера при a=0,05 и степенях свободы f₁ = N-1 и f₂ = N-L (F_т = 19,2). Точность описания (коэффициент детерминации R²) реальной зависимости найденным линейным уравнением регрессии составляет 95 %.

Подобные расчеты были выполнены на ПЭВМ с помощью статистического пакета STATGRAPHICS [7] не только для семейства прямых, но и некоторых других функций (табл. 15).

Данные табл. 15 показывают, что выход нитробензола зависит от времени его синтеза и эта зависимость с наибольшей вероятностью (Р» 0,983) описывается линейным уравнением вида

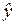= - 107 + 1,3 х.

Оба коэффициента уравнения регрессии (а = - 107 и b = 1,3) с вероятностью Р > 0,96 являются "значимыми" (т.е. не равными нулю), так как уровень их значимости равен соответственно a_а = 0,033 и a_b = 0,017.

Таблица 15

Результаты расчетов на ПЭВМ

Функ­ция	Коэф­фици­ент	F-	Адек-
	обо­з­на­­че­ние	значе­ние	S	tт	a	соот- но-ше- ни­	ват-­ но­сть (a)
y = a + b x	a b	- 107 1,3	20,013 0,173	- 5,347 7,506	0,033 0,017	56,33	0,017
y = e(a+b x)	a b	- 0,3741 0,03519	0,9969 0,0086	-0,375 4,078	0,744 0,055	25,88	0,055
1/ y = a + b x	a b	0,14867 -0,00105	0,0423 0,0004	3,5128 -2,867	0,072 0,103	11,07	0,103

Более подробно с проведением классического регрессионного
анализа для практических целей можно ознакомиться в [11].

5.3.2.2. Математическое планирование эксперимента для проведения регрессионного анализа

В современных условиях, учитывая многогранность изучаемых явлений, острый дефицит времени, высокую стоимость эксплуатации научного оборудования, необходимо стремиться к наиболее рациональным планам проведения эксперимента.

Применение методов математического планирования эксперимента для проведения регрессионного анализа (РАМПЭ) приводит к увеличению точности получаемого уравнения регрессии, а иногда и к значительному сокращению числа опытов.

В основу методов математического планирования эксперимента для проведения РА положен принцип "черного ящика". Суть этого принципа заключается в том, что исследователь, не зная об истинных закономерностях поведения объекта, описывает его с помощью статистических математических моделей.

Образно говоря, "ударяя" по исследуемому объекту изменением входных параметров (x _j) в ходе эксперимента (рис. 6) и измеряя его реакцию (y _v) на эти "удары" при действии случайных факторов (w_z), можно получить статистическую математическую зависимость, пригодную для прогноза поведения объекта.

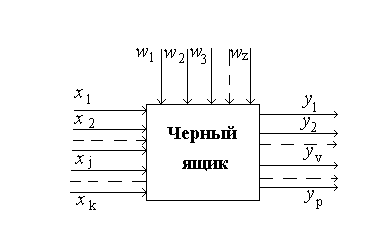
Рис. 6. Схема объекта по принципу "черного ящика"

В отличие от детерминированных математических моделей объекта, построенных на основе фундаментальных законов физики, механики, химии или других, статистические математические модели получают, описывая зависимости выходных параметров (свойств, откликов) объекта от изменения входных параметров (факторов) с помощью полиномов различной степени.

Статистической математической моделью объекта является функция или набор функций, описывающих зависимость величин выходных параметров (свойств, отклика) объекта (y_v) от значений входных параметров (x _j):

y_v = j_v(x ₁, x ₂, x ₃,..., x _j,..., x _k) + e(w₁, w₂, w₃,..., w_z,...),

где e - вклад в изменение свойств объекта случайных факторов.

Наиболее часто в качестве статистической модели объекта используют приближенные уравнения регрессии:

.

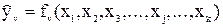Известно, что любую функцию (в том числе j и f) можно разложить в ряд Тейлора и представить в виде конкретного полинома определенной степени (конечного отрезка ряда Тейлора) вида:

…,

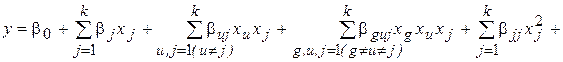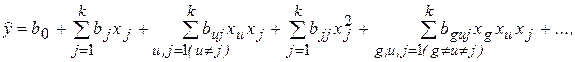
где b и b - соответственно генеральные и выборочные коэффициенты ряда Тейлора.

По результатам эксперимента возможно определить вид полинома только с выборочными коэффициентами, которые характеризуют:

b₀ - величину y при нулевом значении всех факторов (свободный член);

b₁, b₂,..., b_j,..., b_k - линейные эффекты влияния соответствующих факторов на величину y;

b₁₂, b₁₃,..., b_1j,...,b_1k, b₂₃, b₃₄,..., b_2j,..., b_(k-1)j, ..b_(k-1)k - парные эффекты влияния соответствующих факторов на величину y (эффекты "взаимодей­ствия" двух соответствующих факторов);

b₁₁, b₂₂,..., b_jj,..., b_kk - квадратичные эффекты влияния соответствующих факторов на величину y;

b₁₂₃, b₁₂₄,..., b_1uj,..., b₂₃₄, b₂₃₅,..., b_2uj,..., b_(k-2)(k-1)k - тройные эффекты влияния соответствующих факторов на величину y (эффекты "взаимодей­ствия" трех соответствующих факторов) и т.д.

Наиболее удобно планировать эксперимент математическими методами для кодированных значений факторов (x _j), получаемых из натуральных значений (X _j) по следующим формулам:

; ; ,
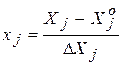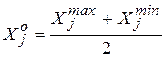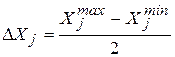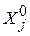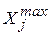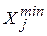где - натуральное значение фактора в центре (середине) выбранной (заданной) области изменения (варьирования) фактора, и - соответственно максимальное и минимальное значения фактора в выбранной области его изменения. В соответствии с этими формулами натуральному значению X _j = 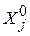соответствует кодированное значение x _j = 0; X _j = 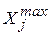- кодированное значение x _j = +1, а X _j = 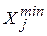- значение x _j = -1.

Переход от кодированных значений факторов к натуральным осуществляют по формуле

.

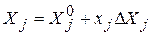Выбор плана эксперимента для применения РАМПЭ в отличие от планирования экспериментов для проведения КРА определяется видом выбранного семейства функций (видом полинома).

После завершения эксперимента для проведения РАМПЭ выполняют следующие действия:

Выбирают вид полинома (отрезок ряда Тейлора) для поиска уравнения регрессии.

Для выбранного полинома с помощью МНК рассчитывают параметры функции (выборочные коэффициенты уравнения регрессии).

Проверяют рассчитанные выборочные коэффициенты уравнения регрессии на значимость (равенство нулю).

Корректируют вид исходной функции, исключая из нее незначимые коэффициенты и другие составляющие.

Оценивают ошибки, допускаемые при описании истинной зависимости j с помощью найденного уравнения регрессии: проверяют адекватность уравнения регрессии с помощью распределения Фишера или рассчитывают вероятность описания зависимости j функцией f.

Если точность найденного уравнения регрессии не удовлетворяет, то выбирают, планируют и реализуют другой план эксперимента для поиска уравнения регрессии в другом семействе полиномов (например, полиномов более высокого порядка).

Порядок проведения РАМПЭ в отличие от КРА имеет следующие особенности:

Выбирается только один класс функций - полиномы.

Используется только один метод приближения - МНК.

После корректировки уравнения регрессии его коэффициенты не пересчитываются.

Выполняется меньшее количество этапов РА.

Обычно поиск уравнения регрессии начинают в семействе самых простых полиномов: первого и второго порядка. По названиям степеней полиномов называют и планы эксперимента для применения РАМПЭ.

Прежде чем перейти к знакомству с методами математического планирования эксперимента для применения регрессионного анализа, необходимо отметить некоторые важные обстоятельства [8]:

1. С познавательной точки зрения полиноминальная статистическая модель объекта не представляет большого интереса. Зная оценки коэффициентов отрезков ряда Тейлора, нельзя определить истинную зависимость j, а следовательно, невозможно получить информацию о механизме поведения исследуемого объекта.

2. Полиноминальные модели справедливы только для условий, в которых проводился эксперимент.

3. Полиноминальные модели очень полезны с практической точки зрения, так как позволяют управлять поведением объекта и решать для него задачи оптимизации.

Планы первого порядка

Планы первого порядка позволяют находить линейные уравнения регрессии (I) и нелинейные уравнения (II) с членами, учитывающими эффекты "взаимодействия" факторов:

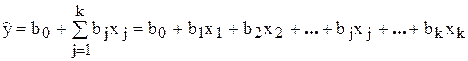; (I)

=

=

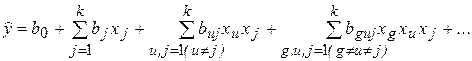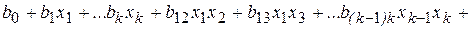
+ b ₁₂₃ x ₁ x ₂ x ₃ + b ₁₂₄ x ₁ x ₂ x ₄+...+ b _{(k-2) (k-1) k} x _k-2 x _k-1 x _k. (II)

Для удобства программирования расчетов вводят в состав уравнения регрессии фиктивную переменную х₀ = +1 во всех опытах эксперимента:

;

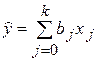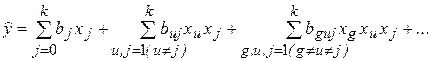
Для РАМПЭ наибольшее распространение получили двухуровневые (m_j = m =2) ортогональные D-оптимальные планы первого порядка типа
2^(c-a). При таких планах все факторы в кодированном виде могут иметь только два значения (x _j = +1 и x _j = -1). Тип плана обозначает формулу для расчета числа его опытов без их повторения (N): N = m^(c-a) = 2^(c-a), где c > a, c ³ k и а равно 0,1, 2, 3,...

При а = 0 такой план типа 2^(c-a) является планом ПФЭ, а при а > 0 - планом ДФЭ.

Планы, отвечающие условиям ортогональности, позволяют любой коэффициент уравнения регрессии рассчитывать по одной формуле:

,

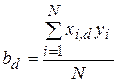где i - номер опыта в плане эксперимента; b_d - коэффициент, учитывающий эффект факторов, значения которых приведены в столбце x _d плана эксперимента; y_i - свойства объекта, измеренные при проведении соответствующего опыта; N - число опытов в эксперименте.

D-оптимальные планы обеспечивают минимальную и одинаковую ошибку в оценке всех коэффициентов уравнения регрессии (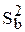), определяемую по формуле

,

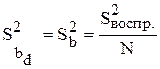где 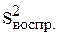- дисперсия воспроизводимости, характеризующая случайные ошибки всего эксперимента.

Условием ортогональности плана эксперимента является выполнение условия

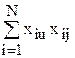= 0 при u ¹ j и u,j равных 0, 1, 2,..., k.

Для D- оптимальных планов должны выполняться следующие условия:

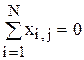при j равном 1, 2,..., k;

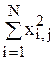= N при j равном 0, 1, 2,..., k.

Выбор плана эксперимента начинается с расчета необходимого числа опытов (N_необх.) или его задания (N_зад.). При этом должны выполняться соотношения

N ³ N_необх.; N_необх. ³ k + 1; N_необх. ³ L + 1; N_зад. ³ N,

где L - общее число коэффициентов в выбранном семействе полиномов.

При расчете N_необх. задаются видом полинома (типом и числом коэффициентов уравнения регрессии L), а при задании числа опытов определяют вид семейства полиномов, в котором возможно найти уравнение регрессии для данного числа опытов в эксперименте:

k_max = N_зад. - 1; L_max = N_зад. -1.

Рассмотрим возникающие задачи выбора линейного плана на примере.

Допустим, что мы решили исследовать влияние на свойство y четырех факторов x _j (k = 4) и описать их зависимость уравнением регрессии в виде следующего нелинейного полинома (L = 11):

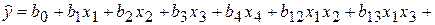
+ b ₁₄ x ₁ x ₄ + b ₂₃ x ₂ x ₃ + b ₂₄ x ₂ x ₄ + b ₃₄ x ₃ x ₄.

Тогда совместное выполнение соотношений даст:

N_необх. ³ k + 1 ³ 4+1 ³ 5; N_необх. ³ L + 1 ³ 11+1 ³ 12; N_необх. ³ 12.

Очевидно, что соотношению N ³ N_необх отвечают планы типа 2^(с-а) при условии, что (с-a) ³ 4 и соответственно N ³ 16. Из совокупности планов с N ³ 16 выберем план ПФЭ типа 2⁴ как наиболее экономный по числу опытов (N = 16) и позволяющий получить наиболее точные оценки коэффициентов уравнения регрессии. При ПФЭ все выборочные коэффициенты уравнения регрессии являются достаточно точными, "несмешанными" оценками соответствующих генеральных коэффициентов: b_d» b_d.

Для построения ортогонального и D-оптимального плана ПФЭ типа 2⁴ воспользуемся одним из распространенных приемов, заключающемся в следующем:

Делается заготовка плана в виде таблицы (плана-матрицы эксперимента), в которой предусматривается не менее N строк и (L+2) столбца.

В первый столбец таблицы заносят номера строк, соответствующие номерам опытов. Во второй столбец - кодированные значения фиктивного фактора х ₀ = + 1. В третий столбец - кодированные значения первого фактора в виде последовательного чередования друг за другом значений (+1) и (-1). В последующем, четвертом столбце, выбранная комбинация чередований в предыдущем столбце знаков (+1) и (-1) удваивается, например: после двух знаков (+1) следуют два знака (-1). По аналогичному принципу удвоения комбинации чередования знаков предыдущего столбца заполняются и последующие столбцы для всех оставшихся факторов.

Столбцы для оценки эффектов "взаимодействия" факторов заполняются путем перемножения знаков для соответствующих факторов в соответствующих строках таблицы.

Правильность составления плана проверяется по выполнению условия его D- оптимальности .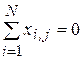

Построенный по этому приему план приведен в табл. 16.

Таблица 16

План эксперимента типа 2⁴

Но-	Кодированные значения факторов	y
мер опы­та i	х0	х1	х2	х3	х4	х12	х13	х14	х23	х24	х34
	+1	+1	+1	+1	+1	+1	+1	+1	+1	+1	+1
	+1	-1	+1	+1	+1	-1	-1	-1	+1	+1	+1
	+1	+1	-1	+1	+1	-1	+1	+1	-1	-1	+1
	+1	-1	-1	+1	+1	+1	-1	-1	-1	-1	+1
	+1	+1	+1	-1	+1	+1	-1	+1	-1	+1	-1
	+1	-1	+1	-1	+1	-1	+1	-1	-1	+1	-1
	+1	+1	-1	-1	+1	-1	-1	+1	+1	-1	-1
	+1	-1	-1	-1	+1	+1	+1	-1	+1	-1	-1
	+1	+1	+1	+1	-1	+1	+1	-1	+1	-1	-1
	+1	-1	+1	+1	-1	-1	-1	+1	+1	-1	-1
	+1	+1	-1	+1	-1	-1	+1	-1	-1	+1	-1
	+1	-1	-1	+1	-1	+1	-1	+1	-1	+1	-1
	+1	+1	+1	-1	-1	+1	-1	-1	-1	-1	+1
	+1	-1	+1	-1	-1	-1	+1	+1	-1	-1	+1
	+1	+1	-1	-1	-1	-1	-1	-1	+1	+1	+1
	+1	-1	-1	-1	-1	+1	+1	+1	+1	+1	+1

Нетрудно проверить, что данный план является ортогональным и D-оптимальным.

План с натуральными значениями факторов строится исходя из плана с кодированными значениями путем замены знаков (+1) и (-1) на соответствующие им натуральные значения для данного фактора.

Довольно часто на практике приходится задаваться не видом полинома, а числом опытов из-за дефицита ресурсов для проведения эксперимента (времени, средств и др.). В этом случае выбор плана эксперимента начинают с расчета параметров полинома, которые возможно определить при N_зад.

Допустим, что N_зад. = 10. Тогда:

k_max = N_зад. - 1= 10-1= 9;

L_max = N_зад. -1= 10-1= 9.

Из данных равенств следует, что план с 10 опытами позволяет решить нашу задачу и оценить влияние четырех факторов (k < k_max) по уравнению регрессии в виде полинома с числом коэффициентов не более 9. Исходя из этого выберем для поиска уравнения регрессии линейный полином вида

(L = 5):

.

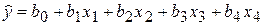Для четырех факторов план ПФЭ насчитывает 16 опытов: 2^k = 2⁴ = 16. Поэтому при N_зад. = 10 возможна реализация только плана ДФЭ типа 2^(k-a). Наиболее близким по числу опытов к N_зад. = 10 является полуреплика (1/2 часть) плана ПФЭ, т.е. план ДФЭ типа 2^(4-1) с числом опытов N = 8. Проверка показывает, что план типа 2^(4-1) пригоден для решения поставленной задачи, так как выполняются следующие соотношения:

N ³ k + 1 ³ 4+1 ³ 5;

N ³ L + 1 ³ 5+1 ³ 6.

Поскольку план ДФЭ представляет собой часть опытов плана ПФЭ, то необходимо решить, какой именно набор опытов из плана ПФЭ использовать в плане ДФЭ. От этого набора будет зависеть точность определения эффектов влияния факторов на свойство y (так называемая "смешиваемость" коэффициентов).

Построение планов ДФЭ начинают по тому же приему, что и при построении планов ПФЭ для числа факторов, равных разности (k-а):

k-a = 4-1 = 3.

Поэтому построим первоначально заготовку плана ДФЭ типа

2^(4-1) в виде плана ПФЭ типа 2³, предусмотрев в нем (L+2 = 11+2 = 13) колонок (табл. 17).

При заполнении столбца для фактора х₄ принцип удвоения чередований уровней не подходит, так как его использование в данном столбце даст только знаки (+1) и такой план не будет являться ортогональным.

Таблица 17

Заготовка плана ДФЭ типа 2^(4-1)

Но-

Кодированные значения факторов

y

мер опы­та i

х0

х1

х2

х3

х4

х12

х13

х14

х23

х24

х34

+1

+1

+1

+1

+1

-1

+1

+1

+1

+1

-1

+1

+1

-1

-1

+1

+1

+1

+1

-1

+1

-1

+1

-1

+1

+1

-1

-1

+1

-1

-1

-1

Если же для заполнения столбца х ₄ воспользоваться произведением двух и более других факторов в одной строке плана (так называемым генерирующим соотношением), то тогда план будет и ортогональным и D- оптимальным.

К выбору генерирующего соотношения нужно подходить осознанно, так как оно определяет "смешанность" коэффициентов уравнения регрессии, полученных по составленному плану.

Исходя из этого составим все возможные варианты генерирующего соотношения для х ₄:

х ₄ = х ₁ х ₂ (I); x ₄ = x ₁ x ₃ (II); x ₄ = x ₂ x ₃ (III); x ₄ = x ₁ x ₂ x ₃ (IV).

Для данных генерирующих соотношений рассчитаем определяющие контрасты путем умножения левой и правой частей соответствующего генерирующего соотношения на х ₄:

; ; ; .

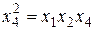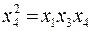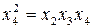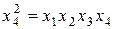Так как х ₄ = ± 1, то 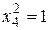и определяющие контрасты можно выразить равенствами:

1 = х ₁ х ₂ х ₄ (I); 1 = х ₁ х ₃ х ₄ (II); 1 = x ₂× x ₃× x ₄ (III); 1 = x ₁× x ₂× x ₃× x ₄ (IV).

Можно определить в плане столбцы с одинаковым порядком чередования знаков (+1) и (-1), перемножив левые и правые части определяющих контрастов на каждый фактор, например для фактора х ₁:

; ;

; .

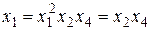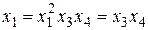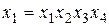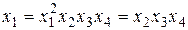Эти равенства показывают, что при генерирующих соотношениях I-IV выборочный коэффициент b₁ будет служить оценкой влияния на y не только фактора x ₁, но и других:

b₁» b₁ + b₂₄ (I); b₁» b₁ + b₃₄ (II); b₁» b₁ + b₁₂₃₄ (III); b₁» b₁ + b₂₃₄ (IV).

Эффекты "взаимодействия" трех и более факторов обычно близки к нулю и ими можно пренебрегать:

b₁» b₁ + b₂₄ (I); b₁» b₁ + b₃₄ (II); b₁» b₁(III); b₁» b₁(IV).

Поэтому можно считать, что "несмешанные" оценки эффекта влияния фактора x ₁ на свойство y могут быть получены при реализации плана ДФЭ с генерирующими соотношениями III и IV для фактора х₄. Результаты проверки на "смешиваемость" остальных эффектов приведены в табл. 18.

Таблица 18

Параметры проверки разрешающей силы дробной реплики типа 2^(4-1)

Параметр	Выражение для определения параметра
Генери­рую­щее соотно­шение	x 4 = x 1 x 2 (I)	x 4 = x 1 x 3 (II)	x 4 = x 2 x 3 (III)	x 4 = x 1 x 2 x 3 (IV)
Опреде­ля­ю­щий контраст	1 = x 1 x 2 x 4	1 = x 1 x 3 x 4	1 = x 2 x 3 x 4	1 = x 1 x 2 x 3 x 4
Оценки коэффи­циентов уравне­ния регрессии	b0» b0+b124 b1» b1 + b24 b2» b2 + b14 b3» b3 + b1234 b4» b4 + b12 b12» b12+b4 b13» b13+b234 b14» b14+b2 b23» b23+b134 b24» b24+b1 b34» b34+b123	b0» b0+b134 b1» b1 + b34 b2» b2 + b1234 b3» b3 + b14 b4» b4 + b13 b12» b12+b234 b13» b13+b4 b14» b14+b3 b23» b23+b124 b24» b24+b123 b34» b34+b1	b0» b0+b234 b1» b1 + b1234 b2» b2 + b34 b3» b3 + b24 b4» b4 + b23 b12» b12+b134 b13» b13+b124 b14» b14+b123 b23» b23+b4 b24» b24+b3 b34» b34+b2	b0» b0+b1234 b1» b1 + b234 b2» b2 + b134 b3» b3 + b124 b4» b4 + b123 b12» b12+b34 b13» b13+b24 b14» b14+b23 b23» b23+b14 b24» b24+b13 b34» b34+b12
Примечание. Жирным шрифтом выделены "несмешанные" коэффициенты

Данные табл. 18 показывают, что при любом генерирующем соотношении точными ("несмешанными") будут пять коэффициентов. Для генерирующего соотношения I точными будут все коэффициенты, оценивающие эффект фактора х₃, при II - эффект фактора х₂, при III - эффект фактора х₁, а при IV - линейные эффекты всех факторов.

Допустим, что нас больше всего интересует точность линейных эффектов всех факторов. Поэтому выбираем генерирующее соотношение IV и в соответствии с ним заполняем колонку плана для х ₄ и остальные колонки (табл. 19).

Этот план, с N = 8, является ортогональным и D-оптимальным, однако, как показывают и данные табл. 18, в нем есть столбцы с совпадающими комбинациями знаков (х ₁₄ и х ₂₃, х ₁₃ и х ₂₄ и др.), что приведет к получению "смешанных" коэффициентов уравнения регрессии (т.е. неточно отражающих влияние соответствующих факторов).

Таблица 19

План ДФЭ типа 2^(4-1) с генерирующим соотношением x ₄ = x ₁ x ₂ x ₃

Но-

Кодированные значения факторов

y

мер опы­та i

х0

х1

х2

х3

х4

х12

х13

х14

х23

х24

х34

+1

+1

+1

+1

+1

+1

+1

+1

+1

+1

+1

+1

-1

+1

+1

-1

-1

-1

+1

+1

-1

-1

+1

+1

-1

+1

-1

-1

+1

-1

-1

+1

-1

+1

-1

-1

+1

+1

+1

-1

-1

-1

-1

+1

+1

+1

+1

-1

-1

+1

-1

-1

-1

-1

+1

+1

-1

+1

-1

+1

-1

+1

-1

-1

+1

-1

+1

+1

-1

-1

+1

-1

-1

+1

+1

-1

-1

+1

-1

-1

-1

-1

+1

+1

+1

+1

+1

+1

Оставшиеся два опыта (опыты № 9 и № 10) можно использовать как повторные для оценки дисперсии воспроизводимости эксперимента, если сделать допущение, что и другие опыты плана имеют такие же случайные ошибки. Дисперсия воспроизводимости (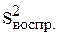) может быть использована для оценки ошибки в определении коэффициентов уравнения регрессии и их значимости, а также проверки адекватности найденного уравнения регрессии.

В соответствии с общепринятыми рекомендациями запланируем опыты для определения 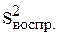при нулевых кодированных значениях всех исследуемых факторов, т.е. в центре плана эксперимента (табл. 20).

В качестве планов первого порядка для проведения РАМПЭ можно использовать не только дробные реплики ПФЭ, но и некоторые другие планы ДФЭ, например планы Плакетта-Бермана.

Следует только еще раз повторить, что прежде, чем использовать планы ДФЭ, необходимо оценить потерю точности в определении эффектов влияния факторов на свойство объекта.

Алгоритмы расчетов при РАМПЭ по планам первого порядка зависят от наличия повторений опытов. Познакомьтесь с ними самостоятельно [8].

После реализации плана эксперимента первого порядка довольно часто найденное уравнение регрессии оказывается неадекватным. В этом случае обычно переходят к выполнению РАМПЭ для поиска уравнения регрессии в семействе полиномов второго порядка по результатам специально спланированных экспериментов.

Таблица 20

План ДФЭ типа 2^(4-1) с опытами для определения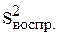

Но-

Кодированные значения факторов

y

мер опы­та i

х0

х1

х2

х3

х4

х12

х13

х14

х23

х24

х34

+1

+1

+1

+1

+1

+1

+1

+1

+1

+1

+1

+1

-1

+1

+1

-1

-1

-1

+1

+1

-1

-1

+1

+1

-1

+1

-1

-1

+1

-1

-1

+1

-1

+1

-1

-1

+1

+1

+1

-1

-1

-1

-1

+1

+1

+1

+1

-1

-1

+1

-1

-1

-1

-1

+1

+1

-1

+1

-1

+1

-1

+1

-1

-1

+1

-1

+1

+1

-1

-1

+1

-1

-1

+1

+1

-1

-1

+1

-1

-1

-1

-1

+1

+1

+1

+1

+1

+1

+1

+1

Планы второго порядка

Существуют различные виды планов второго порядка: трехуровневые планы типа 3^k, планы Бокса, Бокса-Уилсона, Бокса-Хантера и др. Эти планы позволяют найти уравнение регрессии в следующем семействе полиномов второго порядка:

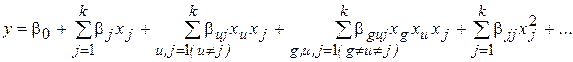
Популярностью пользуются композиционные планы Бокса-Уилсона, как наиболее экономные по числу опытов и включающие в себя составной частью планы первого порядка: типа 2^k (при k < 5) и 2^(k-1) (при k ³ 5).

Общее число опытов плана Бокса-Уилсона (N_БУ) рассчитывается по следующим формулам:

N_БУ = N_ПФЭ + N^* + n₀ = 2^k + 2k + n₀ (при k < 5);

N_БУ = N_ДФЭ + N^* + n₀ = 2^k-1 + 2k + n₀ (при k ³ 5),

где N_ПФЭ и N_ДФЭ - число опытов плана первого порядка; N^* - число опытов в "звездных" точках; n₀ - число опытов при нулевых кодированных значениях всех исследуемых факторов (задается исследователем!).

Построение плана Бокса-Уилсона начинается с построения входящего в его состав плана первого порядка (табл. 21).

После заполнения всех строк плана первого порядка (N_ПФЭ или N_ДФЭ) заполняют 2k строк для "звездных точек" плана.

Звездные точки располагаются на координатных осях соответствующих факторов на расстоянии l ³ 1 от начала координат (см. табл. 21).

Для получения ортогонального плана величина l (величина "звездно­го пле­ча") рассчитывается по формулам:

l⁴ + 2^k l² - 2^(k-1) (k + 0,5n_o) = 0 (при k < 5);

l⁴ + 2^(k-1)l² - 2^(k-2) (k + 0,5n_o) = 0 (при k ³ 5).

На основании этих формул составлены таблицы для l² при различных величинах k и n₀. Так, например, из таблицы [8] при k = 2 величина l² = 1 (при n₀ = 1) и l² = 1,160 (при n₀ = 2).

После заполнения строк для "звездных точек" плана Бокса-Уилсона заполняют строки с нулевыми кодированными значениями всех исследуемых факторов (число строк равно n₀).

Затем к плану добавляется k столбцов для преобразованных значений 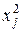(х '), необходимых для проведения расчетов при РАМПЭ. Эти столбцы заполняются значениями, рассчитанными по формуле

.

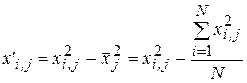Пример плана Бокса-Уилсона для k = 2 и n₀ = 2 приведен в табл. 21.

Таблица 21

План Бокса-Уилсона при k = 2 и n₀ = 2

Но-	Значения факторов	yi
мер опы-	кодированные	натуральные
­та i	x0	x1	x2	х 12	x'1	x'2	Х1	Х2
	+1	+1	+1	+1	0,368	0,368
	+1	-1	+1	-1	0,368	0,368
	+1	+1	-1	-1	0,368	0,368
	+1	-1	-1	+1	0,368	0,368
	+1	+1,077			0,528	-0,632
	+1	-1,077			0,528	-0,632
	+1		+1,077		-0,632	0,528
	+1		-1,077		-0,632	0,528
	+1				-0,632	-0,632
	+1				-0,632	-0,632

Алгоритмы проведения РАМПЭ по планам Бокса-Уилсона изучите самостоятельно [8,12,13].

Как уже отмечалось ранее, РА проводят для факторов только с количественными значениями. Для решения задач по оценке влияния на свойства объекта одновременного действия количественных и качественных факторов можно применять принципы регрессионного и дисперсионного анализов, используя сложные планы эксперимента типа 2^2k. Например, сложный план типа 2^2×2 позволяет исследовать влияние на свойство y одновременно 3 качественных факторов на 4 уровнях и до 12 количественных факторов на 2 уровнях. Познакомьтесь с построеним таких планов и их применением самостоятельно [8].

Планирование эксперимента для решения оптимизационных задач

Оптимизационные задачи в большинстве случаев формулируются как задачи поиска экстремальных значений функции отклика объекта (максимумов или минимумов). Например, инженеру часто приходится решать задачи поиска оптимальных условий производства продукции с максимальной производительностью или минимальной себестоимостью.

Поведение объекта во многих случаях приходится описывать несколькими функциями отклика. Очень редко удается найти такое сочетание значений всех влияющих факторов, при котором достигаются все желаемые экстремумы функций отклика объекта. Большинство влияющих факторов можно изменять только в реальных пределах: концентрации реагентов не могут быть отрицательными, температуры процессов не могут превышать безопасные значения и т.д. Исследователю нужны и реальные значения функции отклика объекта: неотрицательные значения выхода продукции, степени очистки, себестоимости продукции и др. Поэтому в большинстве случаев оптимизационные задачи решают при условии различных ограничений на величину влияющих факторов и значений функций откликов объектов, т.е. проводят поиск рациональны х значений влияющих факторов.

При традиционном поиске рациональных условий стабилизируют все факторы, кроме одного. При этом зачастую обнаруживается только часть экстремальных значений функции отклика объекта («локальные» экстремумы).

Для получения более полной информации о поведении объекта рекомендуется проводить поиск рациональных условий при одновременном изменении нескольких факторов, используя специальные методы математического планирования эксперимента [8,12-15].

Все методы математического планирования эксперимента для решения оптимизационных задач делят на две группы: методы, требующие знаний уравнения регрессии функции отклика объекта, и методы, не требующие таких знаний.

К группе методов, требующих знаний уравнения регрессии функции отклика объекта, относятся:

метод крутого восхождения или наискорейшего спуска по поверхности функции отклика объекта;

метод обобщенной функции желательности и др.

К другой группе методов относится симплекс-метод, или метод симплекс-планирования эксперимента.

Коротко рассмотрим суть некоторых из этих методов.

5.4.1. Метод крутого вос х ождения или наискорейшего спуска по повер х ности функции отклика объекта

Применение данного метода начинается с получения функции отклика объекта в виде исходного уравнения регрессии. Для этого выбирают влияющие факторы и области их изменения (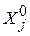, D X _j), планируют и реализуют план эксперимента первого или второго порядка.

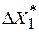После нахождения исходного уравнения регрессии определяют шаг и направление поиска экстремума функции отклика объекта. Для этого один из факторов принимают за базовый и для него выбирают шаг движения, который должен быть не больше шага варьирования этого фактора при получении исходного уравнения регрессии (D Х _j), например, если за базовый фактор взять Х ₁, то для базового шага движения () должно выполняться соотношение .

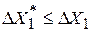Шаги движения остальных факторов рассчитывают следующим образом:

; ,

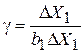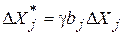где b_j – линейные эффекты факторов (с учетом их знаков!) в исходном уравнении регрессии.

Движение к экстремуму функции отклика объекта начинают из центра плана эксперимента, использованного при получении исходного уравнения регрессии (X _j = 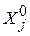, x _j = 0).

При поиске максимума функции отклика объекта (метод крутого восхождения) для определения условий проведения последующего опыта к координатам предыдущего опыта в факторном пространстве прибавляют шаги движения по каждому фактору. При поиске минимума (метод наи­скорейшего спуска) из координат предыдущего опыта вычитают шаги движения.

Движение к экстремуму прекращают в следующих случаях:

1. Значения функции отклика объекта или хотя бы одного фактора вышли за пределы допустимых значений.

2. Найден экстремум (возможно, локальный) функции отклика объекта.

В первом случае оптимизацию заканчивают. Во втором случае проводят дополнительные эксперименты по получению нового уравнения регрессии в области обнаруженного экстремума и поиску нового экстремума на основе нового уравнения регрессии.

К недостаткам метода крутого восхождения или наискорейшего спуска следует отнести достаточно большое число экспериментов при его реализации.

С конкретными примерами применения метода крутого восхождения или наискорейшего спуска познакомьтесь самостоятельно по литературе [8,12,13].

5.4.2. Метод симплекс-планирования

Название метода произошло от названия геометрической фигуры "регулярный симплекс", т.е. правильный выпуклый многогранник. Если исследуется влияние на свойство объекта k факторов, то факторное пространство можно задать в виде регулярного симплекса с (k+1) вершиной. Так, например, для двух факторов (k=2) факторное пространство можно задать в виде правильного треугольника (правильный многогранник с 3 вершинами), а для трех факторов (k=3) – в виде тетраэдра (правильный многогранник с 4 вершинами).

Разработаны простые в построении матрицы планов эксперимента с использованием для исследований факторного пространства в виде регулярных симплексов, центр которых совпадает с центром факторного пространства с кодированными значениями факторов (т.е. кординаты центра начального плана эксперимента задаются как x _j = 0) и одна из вершин исходного симплекса лежит на одной из коорди­нат­ных осей этого про­странства. Для такого случая построение плана эксперимента начинается с матрицы Е (матрицы исходного симплекс-плана с кодированными значениями факторов, табл. 22):

Данные табл. 22 показывают, что число опытов в исходном симплекс-плане всегда на единицу больше (N = k+1), чем число исследуемых факторов k.

Таблица 22

Исходный симплекс-план эксперимента с кодированными

значениями факторов

Номер	Кодированные значения факторов	y
опыта i	х1	х2	х3	…	хj	…	xk-1	xk
	e 1	e 2	e 3	…	e j	…	e k-1	e k
	- 1 e 1	e 2	e 3	…	e j	…	e k-1	e k
		-2 e 2	e 3	…	e Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:   24252627282930  Сейчас читают про: Формы, виды и типы культуры Требования безопасности в аварийных ситуациях. Действия работника при возникновении аварийных ситуаций, которые могут привести к несчастным случаям, пожару (взрыву) Закон сохранения момента импульса Орфография и орфограммы. Типы и виды орфограмм КЛАССИФИКАЦИЯ ГЛАСНЫХ ЗВУКОВ РУССКОГО ЯЗЫКА Порядок проведения текущей и генеральной уборки помещений УЗ Самый сильный аргумент, почему эволюция человека не могла быть  Должно говорить правду и избегать многословия © Демокрит ==> читать все изречения... 6546 6232 Понравился сайт? Поделись им с друзьями: