2015-09-06
654
Любая булева функция может иметь бесконечно много представлений в виде ДНФ и КНФ. Особое место среди этих представлений занимают совершенные ДНФ (СДНФ) и совершенные КНФ (СКНФ).
Определение 1. Совершенной ДНФ называется ДНФ, в которой в каждый конъюнкт каждая переменная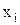 
из набора { 
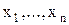}входит ровно один раз, причем входит либо сама 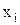, либо ее отрицание 
.
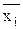Определение 2. Совершенной КНФ называется КНФ, в которой в каждый дизъюнкт каждая переменная 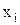из набора { 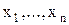}входит ровно один раз, причем входит либо сама 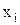, либо ее отрицание .
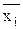Для нахождения СДНФ и СКНФ исходной формулы составляется ее таблица истинности, а затем по ней строится требуемая совершенная нормальная форма. Так, для нахождения СДНФ:
1. Из таблицы истинности выбираем наборы переменных, на которых функция принимает значение 1, и соединяем их конъюнкцией. При этом если переменная принимает значение равное 1, то она входит без отрицания.
2. Все конъюнкции соединяем дизъюнкциями.
Для нахождения СКНФ:
1. Из таблицы истинности выбираем наборы переменных, на которых функция принимает значение 0, и соединяем их дизъюнкцией. При этом если переменная принимает значение равное 0, то она входит без отрицания.
2. Все дизъюнкции соединяем конъюнкциями.
Описанный способ нахождения СДНФ и СКНФ по таблице истинности бывает часто более трудоемким, чем алгоритм, основанный на эквивалентных преобразованиях. Для нахождения СДНФ данную формулу приводим сначала к ДНФ, а затем преобразовываем ее конъюнкты в конституанты единицы с помощью следующих действий:
1. Если в конъюнкт входит некоторая переменная вместе со своим отрицанием, то мы удаляем этот конъюнкт из ДНФ.
2. Если в конъюнкт одна и та же переменнаявходит несколько раз, то удаляем все такие переменные, кроме одной.
3. Если в некоторый конъюнкт не входит некоторая переменная, то в этот конъюнкт, используя закон исключенного третьего, вводим эту переменную путем умножения на единицу, а затем, применяя закон дистрибутивности, приводим полученную формулу к ДНФ.
4. Если в полученной ДНФ имеется несколько одинаковых конъюнктов, то оставляем только один из них.
Описание алгоритма приведения КНФ к СКНФ путем тождественных преобразований аналогично вышеизложенному описанию алгоритма приведения ДНФ к СДНФ. Однако в п.3 введение недостающей переменной осуществляется с помощью закона исключенного третьего путем прибавления нуля.
Кроме того, СКНФ можно получить по найденной СДНФ. Для этого:
1. Получаем отрицание исходной формулы за счет выписывания недостающих конъюнкций через операцию дизъюнкции (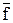
).
2. Выполняем отрицание полученной формулы (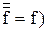
.
Аналогично можно получить СДНФ по найденной ДНФ.
Пример.
Дана функция f(x, y, z) = (x ® y) ¯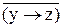 
. Получить СДНФ и СКНФ.
В п. 4.3 получили для f(x, y, z) = (x ® y) ¯ 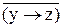ДНФ: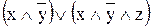 
и КНФ: 
.
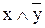Используя преобразование, получим СДНФ:
= 
=
= 
= 
.
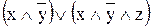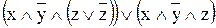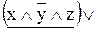
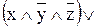
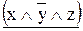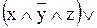
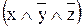Используя преобразование, получим СКНФ:
=
.
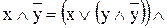
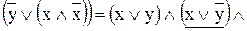
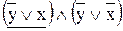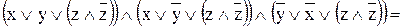
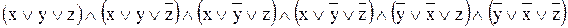Полученные совершенные формы соответствуют таблице истинности (см. п. 4.1).
