Степенная функция

Функция 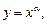где х – переменная величина, a – заданное число, называется степенной функцией.

Если 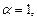то 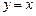– линейная функция, ее график – прямая линия (см. параграф 4.3, рис. 4.7).

Если 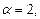то 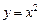– квадратичная функция, ее график – парабола (см. параграф 4.3, рис. 4.8).

Если 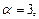то 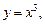ее график – кубическая парабола (см. параграф 4.3, рис. 4.9).

Степенная функция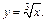

Это обратная функция для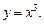

1. Область определения: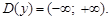

2. Множество значений: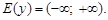

3. Четность и нечетность: функция нечетная.

4. Периодичность функции: непериодическая.

5. Нули функции: x = 0 – единственный нуль.

6. Наибольшее и наименьшее значения функции: наибольшего и наименьшего значений функция не имеет.

7. Промежутки возрастания и убывания: функция является возрастающей на всей области определения.

8. График функции симметричен графику кубической параболы относительно прямой y = x и изображен на рис. 5.1.

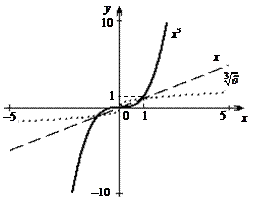Рис. 5.1

Степенная функция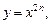

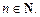
1. Область определения: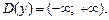

2. Множество значений: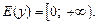

3. Четность и нечетность: функция четная.

4. Периодичность функции: непериодическая.

5. Нули функции: единственный нуль x = 0.

6. Наибольшее и наименьшее значения функции: принимает наименьшее значение для x = 0, оно равно 0.

7. Промежутки возрастания и убывания: функция является убывающей на промежутке 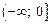и возрастающей на промежутке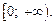

8. График функции (для каждого n Î N) «похож» на график квадратичной параболы 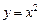(графики функций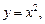 изображены на рис. 5.2).

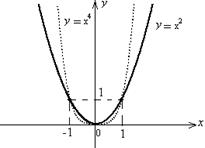
Рис. 5.2

Степенная функция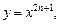

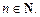
1. Область определения: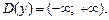

2. Множество значений: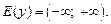

3. Четность и нечетность: функция нечетная.

4. Периодичность функции: непериодическая.

5. Нули функции: x = 0 –единственный нуль.

6. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет при любом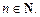

7. Промежутки возрастания и убывания: функция является возрастающей на всей области определения.

8. График функции (для каждого 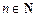) «похож» на график кубической параболы (графики функций 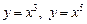изображены на рис. 5.3).

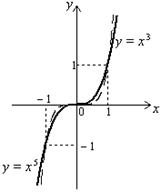Рис. 5.3

Степенная функция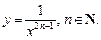

1. Область определения: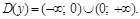

2. Множество значений: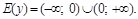

3. Четность и нечетность: функция нечетная.

4. Периодичность функции: непериодическая.

5. Нули функции: нулей не имеет.

6. Наибольшее и наименьшее значения функции: наибольшего и наименьшего значений функция не имеет при любом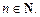

7. Промежутки возрастания и убывания: функция является убывающей в области определения.

8. Асимптоты: 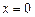(ось Оу) – вертикальная асимптота;

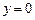(ось Ох) – горизонтальная асимптота.

9. График функции (для любого n) «похож» на график гиперболы (графики функций 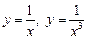изображены на рис. 5.4).

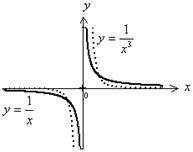Рис. 5.4

Степенная функция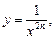

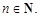
1. Область определения: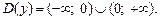

2. Множество значений: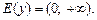

3. Четность и нечетность: функция четная.

4. Периодичность функции: непериодическая.

5. Наибольшее и наименьшее значения функции: наибольшего и наименьшего значений функция не имеет при любом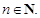

6. Промежутки возрастания и убывания: функция является возрастающей на 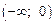и убывающей на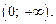

7. Асимптоты: x = 0 (ось Оу) – вертикальная асимптота;

y = 0 (ось Ох) – горизонтальная асимптота.

8. Графиками функций являются квадратичные гиперболы (рис. 5.5).

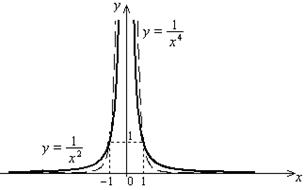Рис. 5.5

Степенная функция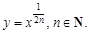

1. Область определения: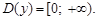

2. Множество значений: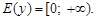

3. Четность и нечетность: функция не обладает свойством четности и нечетности.

4. Периодичность функции: непериодическая.

5. Нули функции: x = 0 –единственный нуль.

6. Наибольшее и наименьшее значения функции: наименьшее значение, равное 0, функция принимает в точке x = 0; наибольшего значения не имеет.

7. Промежутки возрастания и убывания: функция является возрастающей на всей области определения.

8. Каждая такая функция при определенном показателе является обратной для функции 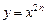при условии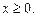

9. График функции «похож» на график функции 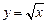при любом n и изображен на рис. 5.6.

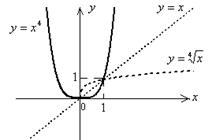
Рис. 5.6

Степенная функция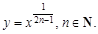

1. Область определения: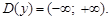

2. Множество значений: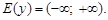

3. Четность и нечетность: функция нечетная.

4. Периодичность функции: непериодическая.

5. Нули функции: x = 0 – единственный нуль.

6. Наибольшее и наименьшее значения функции: наибольшего и наименьшего значений функция не имеет при любом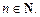

7. Промежутки возрастания и убывания: функция является возрастающей на всей области определения.

8. График функции изображен на рис. 5.7.

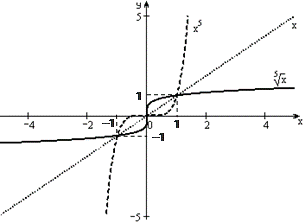Рис. 5.7

Пример 1. Построить график функции:

1) 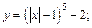2)

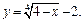
Решение. 1) Для построения графика данной функции используем правила преобразования графиков:

а) строим график функции 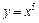(он показан на рис. 5.7);

б) график функции 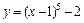получаем из графика функции 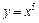путем параллельного переноса его на одну единицу вправо по оси Ох и на две единицы вниз по оси Оу;

в) график исходной функции получаем из графика функции 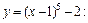оставляем ту часть графика, которая находится справа от оси Оу и на оси Оу, другую – отбрасываем (на рис. 5.8 она показана пунктиром). Оставшуюся часть графика дополняем симметричной ей относительно оси Оу (рис. 5.8).

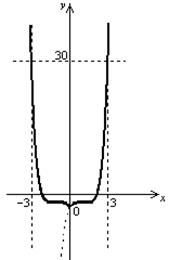
Рис. 5.8

2) Преобразуем функцию к виду 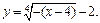Заметим, что 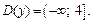График этой функции получаем путем следующих преобразований:

а) строим график функции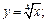

б) график 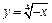получаем из предыдущего симметричным отображением относительно оси Оу;

в) график функции 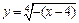получаем из предыдущего смещением на 4 единицы вправо по оси Ох;

г) график заданной функции получаем из графика функции 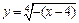параллельным переносом его на две единицы вниз по оси Оу (рис. 5.9).

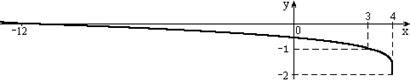Рис. 5.9