Область определения степенной функции

Степенная функция задается формулой y=f(x)=x^a. Область определения степенной функции зависит от значения показателя степени. Перечислим все возможные случаи.

• Если a – положительное целое число, то область определения степенной функции есть множество действительных чисел, то есть, числовой промежуток .
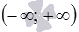• Для всех остальных (нецелых) действительных положительных a областью определения степенной функции является интервал .
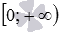• Если a – отрицательное целое число, то область определения степенной функции представляет собой множество .
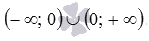• Для всех остальных действительных отрицательных a областью определения степенной функции является числовой промежуток .

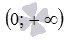При a=0 степенная функция y=f(x)=x^a определена для всех действительных значений x, кроме x=0.

Обратите внимание! Если a - положительная дробь с нечетным знаменателем, то некоторые авторы считают областью определения степенной функции интервал 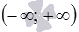, а если a - отрицательная дробь с нечетным знаменателем,- интервал 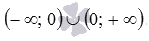. При этом оговариваются, что показатель степени a – несократимая дробь. Сейчас авторы многих учебников по алгебре и началам анализа НЕ ОПРЕДЕЛЯЮТ степенные функции с показателем в виде дроби с нечетным знаменателем при отрицательных значениях аргумента. Мы будем придерживаться именно такого взгляда, то есть, будем считать областями определения степенных функций с дробными положительными и дробными отрицательными показателями степени множества 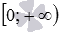и 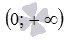соответственно. Рекомендуем учащимся узнать взгляд Вашего преподавателя на этот тонкий момент, чтобы избежать разногласий.

Приведем несколько примеров областей определения степенных функций с различными показателями.

• Областью определения степенных функций является все множество действительных чисел, то есть, .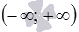
• Степенные функции 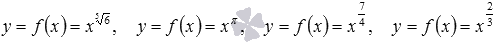определены на интервале .
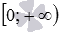• Область определения степенных функций 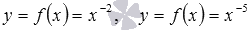- это множество .
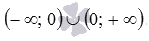• Областью определения степенных функций 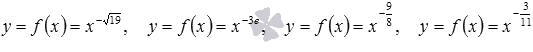является интервал .

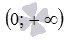К началу страницы