Аналогом дифференциала (первого дифференциала) является в вариационном исчислении вариация (первая вариация):
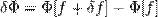
(как и в случае дифференциала имеется в виду линейная часть этого приращения, а выражаясь традиционным образом — 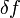 выбирается бесконечно малой, и при вычислении разности отбрасываются бесконечно малые высших порядков). При этом
выбирается бесконечно малой, и при вычислении разности отбрасываются бесконечно малые высших порядков). При этом 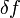 — играющее роль дифференциала или малого приращения независимой переменной — называется вариацией
— играющее роль дифференциала или малого приращения независимой переменной — называется вариацией 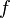 .
.
Как видим, 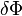 сама в свою очередь является функционалом, так как она, вообще говоря, различна для разных
сама в свою очередь является функционалом, так как она, вообще говоря, различна для разных 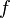 (также и для разных
(также и для разных 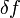 ).
).
Таким образом, это — в применении к функционалам — прямой аналог дифференциала функции конечномерного (в том числе одномерного) аргумента:
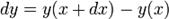
— точно так же понимаемого как линейная часть приращения функции 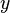 при бесконечно малом приращении аргумента
при бесконечно малом приращении аргумента 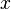 (или линейный член при разложении
(или линейный член при разложении 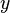 по степеням
по степеням 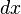 вблизи точки
вблизи точки 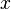 ).
).
 2015-09-06
2015-09-06 254
254







