Как уже было сказано, при плоском поперечном изгибе в поперечном сечении балки возникают два внутренних силовых фактора 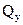 и
и 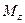 .
.
Перед определением 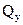 и
и 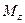 определяют реакции опор балки (рис. 6.3, а), составляя уравнения равновесия статики.
определяют реакции опор балки (рис. 6.3, а), составляя уравнения равновесия статики.
Для определения 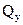 и
и 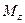 применим метод сечений. В интересующем нас месте сделаем мысленный разрез балки, например, на расстоянии
применим метод сечений. В интересующем нас месте сделаем мысленный разрез балки, например, на расстоянии 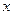 от левой опоры. Отбросим одну из частей балки, например правую, и рассмотрим равновесие левой части (рис. 6.3, б). Взаимодействие частей балки заменим внутренними усилиями
от левой опоры. Отбросим одну из частей балки, например правую, и рассмотрим равновесие левой части (рис. 6.3, б). Взаимодействие частей балки заменим внутренними усилиями 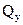 и
и 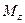 .
.
Установим следующие правила знаков для 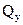 и
и 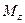 :
:
- Поперечная сила 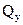 в сечении положительна, если ее векторы стремятся вращать рассматриваемое сечение по часовой стрелке;
в сечении положительна, если ее векторы стремятся вращать рассматриваемое сечение по часовой стрелке;
- Изгибающий момент 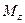 в сечении положителен, если он вызывает сжатие верхних волокон.
в сечении положителен, если он вызывает сжатие верхних волокон.
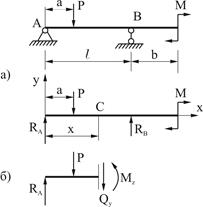
Рис. 6.3
Для определения данных усилий используем два уравнения равновесия:
1. 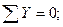
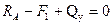 ;
; 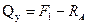 ;
; 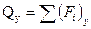 .
.
2. 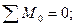
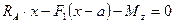 ;
;
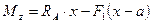 ;
; 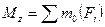
Таким образом,
а) поперечная сила 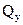 в поперечном сечении балки численно равна алгебраической сумме проекций на поперечную ось сечения
в поперечном сечении балки численно равна алгебраической сумме проекций на поперечную ось сечения 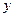 всех внешних сил, действующих по одну сторону от сечения;
всех внешних сил, действующих по одну сторону от сечения;
б) изгибающий момент в поперечном сечении балки численно равен алгебраической сумме моментов (вычисленных относительно центра тяжести сечения) внешних сил, действующих по одну сторону от данного сечения.
При практическом вычислении руководствуются обычно следующим:
1. Если внешняя нагрузка стремится повернуть балку относительно рассматриваемого сечения по часовой стрелке, (рис. 6.4, б) то в выражении для 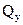 она дает положительное слагаемое.
она дает положительное слагаемое.
2. Если внешняя нагрузка создает относительно рассматриваемого сечения момент, вызывающий сжатие верхних волокон балки (рис. 6.4, а), то в выражении для 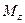 в этом сечении она дает положительное слагаемое.
в этом сечении она дает положительное слагаемое.
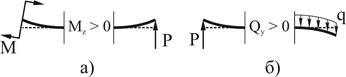
Рис. 6.4
Построение эпюр 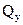 и
и 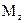 в балках.
в балках.
Рассмотрим двухопорную балку (рис. 6.5, а). На балку действует в точке 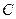 сосредоточенный момент
сосредоточенный момент 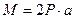 , в точке
, в точке 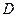 - сосредоточенная сила
- сосредоточенная сила 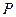 и на участке
и на участке 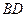 - равномерно распределенная нагрузка интенсивностью
- равномерно распределенная нагрузка интенсивностью 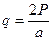 .
.
Определим опорные реакции 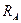 и
и 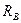 (рис. 6.5, б). Равнодействующая распределенной нагрузки равна
(рис. 6.5, б). Равнодействующая распределенной нагрузки равна 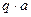 , а линия действия ее проходит через центр участка
, а линия действия ее проходит через центр участка 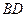 . Составим уравнения моментов относительно точек
. Составим уравнения моментов относительно точек 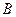 и
и 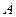 .
.
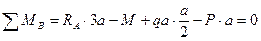
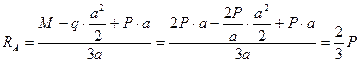
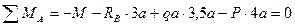
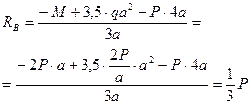
Определим поперечную силу и изгибающий момент в произвольном сечений, расположенном на участке 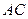 на расстоянии
на расстоянии 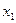 от точки А (рис. 6.5, в). Расстояние
от точки А (рис. 6.5, в). Расстояние 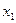 может изменяться в пределах (
может изменяться в пределах (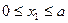 ).
).
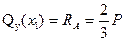 Значение поперечной силы не зависит от координаты сечения Значение поперечной силы не зависит от координаты сечения 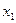 , следовательно, во всех сечениях участка , следовательно, во всех сечениях участка 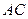 поперечные силы одинаковы и эпюра поперечные силы одинаковы и эпюра 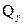 имеет вид прямоугольника. Изгибающий момент изменяется по линейному закону имеет вид прямоугольника. Изгибающий момент изменяется по линейному закону 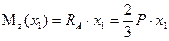 Для построения эпюры вычисляем ординаты на границах участка. При Для построения эпюры вычисляем ординаты на границах участка. При 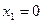 : : 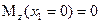 При При 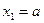 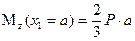 | 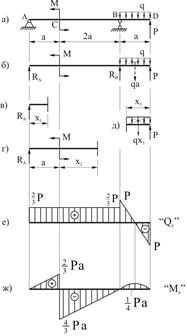 Рис. 6.5 Рис. 6.5 |
Определим поперечную силу и изгибающий момент в произвольном сечений, расположенном на участке 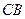 на расстоянии
на расстоянии 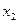 от точки
от точки 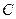 (рис. 6.5, г). Расстояние
(рис. 6.5, г). Расстояние 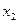 может изменяться в пределах (
может изменяться в пределах (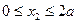 ).
).
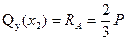
Значение поперечной силы не зависит от координаты сечения 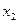 , следовательно, во всех сечениях участка
, следовательно, во всех сечениях участка 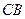 поперечные силы одинаковы и эпюра
поперечные силы одинаковы и эпюра 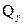 имеет вид прямоугольника. Изгибающий момент
имеет вид прямоугольника. Изгибающий момент
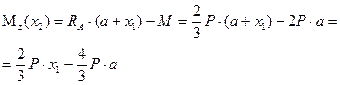
Изгибающий момент изменяется по линейному закону. Определим ординаты эпюры для границ участка.
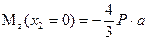
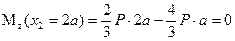
Определим поперечную силу и изгибающий момент в произвольном сечений, расположенном на участке 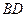 на расстоянии
на расстоянии 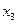 от точки
от точки 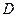 (рис. 6.5, д). Расстояние
(рис. 6.5, д). Расстояние 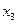 может изменяться в пределах (
может изменяться в пределах (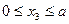 ).
).
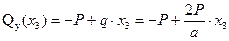
Поперечная сила изменяется по линейному закону. Определим для границ участка.
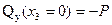
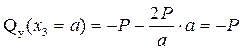
Изгибающий момент
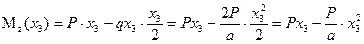 .
.
Эпюра изгибающих моментов на этом участке будет параболической.
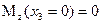
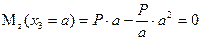
Чтобы определить экстремальное значение изгибающего момента, приравниваем к нулю производную от изгибающего момента по абсциссе сечения 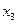 :
:
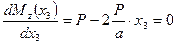
Отсюда
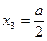
Для сечения с координатой 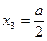 значение изгибающего момента будет составлять
значение изгибающего момента будет составлять
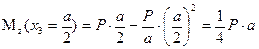
В результате получаем эпюры поперечных сил (рис. 6.5, е) и изгибающих моментов (рис. 6.5, ж).
 2015-09-06
2015-09-06 31574
31574
