В заданный интервал

Лекция 12

Вероятность попадания нормальной случайной величины

в заданный интервал

Уже известно, что если случайная величина X задана плотностью распределения f(x), то вероятность того, что X примет значение, принадлежащее интервалу (а, b), такова:

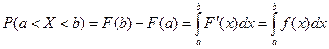
Пусть случайная величина X распределена по нор­мальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу (a,b), равна

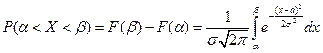
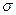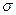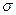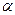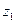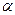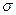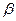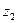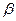Преобразуем эту формулу так, чтобы можно было пользоваться готовыми таблицами. Введем новую пере­менную z = (x - a)/ . Отсюда x = z - a, dx = dz. Найдем новые пределы интегрирования. Если x = , то = ( - а)/ ; если x = , то = ( - a)/ .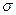

Таким образом

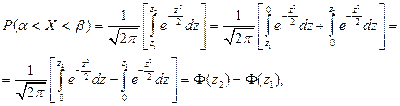
где 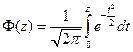- функция Лапласа. Итак

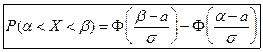(12.1)

Функция Лапласа нечетная функция: Ф(- x) = - Ф(x).

Пример. Случайная величина X распределена по нормальному закону. Математическое ожидание и среднее квадратическое откло­нение этой величины соответственно равны 30 и 12. Найти вероят­ность того, что X примет значение, принадлежащее интервалу (10, 50).

Решение. Воспользуемся формулой (52.2). По условию, 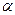=10, 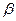= 50, a =30, 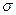=10, следовательно,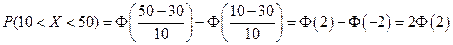

По таблице находим Ф(2) = 0,4772. Отсюда иско­мая вероятность

Р (10 < X < 50) = 2 0,4772 = 0,9544.