Полный расчет балок на прочность при изгибе. Дифференциальное уравнение изогнутой оси
Касательные напряжения при изгибе.
Присутствие поперечных сил при поперечном изгибе свидетельствует о наличии в поперечном сечении касательных напряжений.
В существовании касательных напряжений легко убедиться на следующем простом опыте. Рассмотрим балку, состоящую из двух брусьев, свободно уложенных друг на друга (рис. 7.1, а). Нагрузив ее поперечной силой 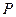 , увидим, что концы верхнего бруса сдвинутся по нижнему брусу и примут ступенчатый вид (рис. 7.1, б). Если эти брусья соединить между собой шпонками, то сдвига между брусьями не произойдет (рис. 7.1, в). Если же эти шпонки окажутся недостаточно прочными, то они могут сколоться, и тогда брусья сдвинутся друг по другу (рис. 7.1, г). В сплошной балке упругие силы, возникающие в продольных слоях балки, противодействуют продольному сдвигу. , увидим, что концы верхнего бруса сдвинутся по нижнему брусу и примут ступенчатый вид (рис. 7.1, б). Если эти брусья соединить между собой шпонками, то сдвига между брусьями не произойдет (рис. 7.1, в). Если же эти шпонки окажутся недостаточно прочными, то они могут сколоться, и тогда брусья сдвинутся друг по другу (рис. 7.1, г). В сплошной балке упругие силы, возникающие в продольных слоях балки, противодействуют продольному сдвигу. | 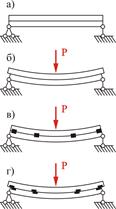 Рис. 7.1 Рис. 7.1 |
Вследствие сдвигов гипотеза плоских сечений при поперечном изгибе нарушается, плоские до деформации сечения слегка искривляются. Влияние указанного эффекта на величину нормальных напряжений невелико и поэтому влиянием сдвигов на закон распределения нормальных напряжений пренебрегают. Поэтому допускаем использование гипотезы плоских сечений и для случая поперечного изгиба.
Рассмотрим консольную балку прямоугольного поперечного сечения, нагруженную сосредоточенной силой 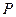 (рис. 7.2, а).
(рис. 7.2, а).
Двумя близкими поперечными сечениями 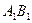 и
и 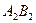 выделим элемент балки длиной
выделим элемент балки длиной 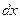 (рис. 7.2, б). Как видно из эпюр, в обоих сечениях
(рис. 7.2, б). Как видно из эпюр, в обоих сечениях 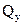 и
и 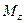 положительны, причем для сечения
положительны, причем для сечения 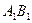
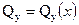 ;
; 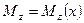 ,
,
а в сечении 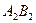
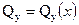 ;
; 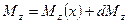 ,
,
Нормальные напряжения на левом и правом торцах выделенного элемента (рис. 7.2, в)
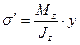
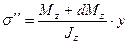 (7.1)
(7.1)
Отсечем часть элемента балки, проведя горизонтальную плоскость 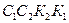 на расстоянии
на расстоянии 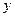 от нейтральной линии (рис. 7.2, в-д).
от нейтральной линии (рис. 7.2, в-д).
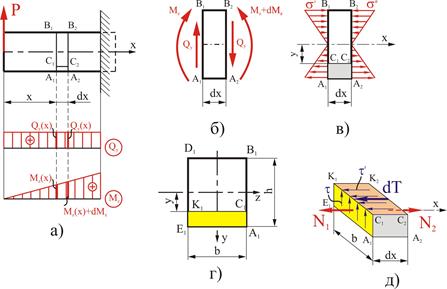 Рис. 7.2 Рис. 7.2 |
Равнодействующая нормальных напряжений 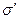 , распределенных по грани
, распределенных по грани 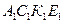 с площадью
с площадью 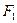
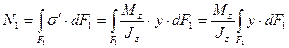
Так как 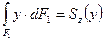 представляет собой статический момент площади
представляет собой статический момент площади 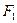
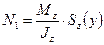 (7.2)
(7.2)
Аналогично в грани 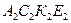 с площадью
с площадью 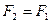 равнодействующая нормальных напряжений
равнодействующая нормальных напряжений 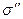
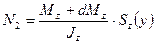 (7.3)
(7.3)
Предположим, что касательные напряжения 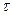 в поперечном сечении параллельны поперечной силе
в поперечном сечении параллельны поперечной силе 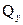 и имеют постоянное значение по ширине сечения на данном уровне (
и имеют постоянное значение по ширине сечения на данном уровне (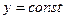 ). Согласно парности касательных напряжений на грани
). Согласно парности касательных напряжений на грани 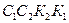 также возникнут касательные напряжения (рис. 7.2, д)
также возникнут касательные напряжения (рис. 7.2, д)
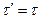
Равнодействующая касательных напряжений 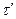
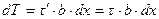
Запишем теперь условие равновесия параллелепипеда 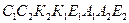
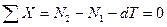
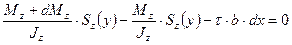
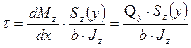 (7.4)
(7.4)
Выведенная зависимость впервые была получена русским ученым Дмитрием Ивановичем Журавским и носит его имя.
Для произвольного сечения (рис. 7.3) величины, входящие в формулу (7.4), имеют следующие значения:
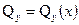 - абсолютная величина поперечной силы в том сечении, где вычисляются касательные напряжения; - абсолютная величина поперечной силы в том сечении, где вычисляются касательные напряжения; 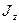 - момент инерции этого сечения относительно его нейтральной линии; - момент инерции этого сечения относительно его нейтральной линии; 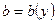 - ширина сечения на уровне, где определяют - ширина сечения на уровне, где определяют 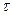 ; ; 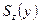 - абсолютная величина статического момента относительно нейтральной линии той - абсолютная величина статического момента относительно нейтральной линии той | 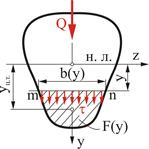 Рис. 7.3 Рис. 7.3 |
части площади 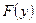 , которая заключена между линией
, которая заключена между линией 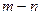 , где определяют
, где определяют 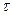 , и краем сечения.
, и краем сечения.
Сделаем общие заключения о распределении касательных напряжений в сечении при поперечном изгибе:
1) вид эпюры 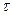 зависит от формы поперечного сечения балки;
зависит от формы поперечного сечения балки;
2) в крайних наиболее удаленных от нейтральной линии точках 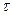 всегда равны нулю;
всегда равны нулю;
3) наибольшей величины касательные напряжения для большинства видов сечений достигают на нейтральной линии сечения, причем
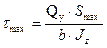 , (7.5)
, (7.5)
где - 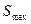 - статический момент половины площади сечения.
- статический момент половины площади сечения.
Формулу (7.5) можно представить в виде
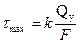 . (7.6)
. (7.6)
Здесь 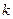 - коэффициент, зависящий от формы сечения. Для прямоугольника
- коэффициент, зависящий от формы сечения. Для прямоугольника 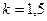 ; для круглого сечения
; для круглого сечения 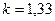 ;
;
4) Формулой Журавского можно пользоваться для вычисления касательных напряжений в любых точках массивных профилей.
 2015-09-06
2015-09-06 4252
4252
