2015-05-13
1106
Для этих поле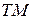й (
или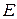 
), как было сказано выше, продольная составляющая напряженности магнитного поля 
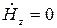. Структура электромагнитного поля для поперечно-магнитных волн находится решением дифференциального уравнения (16) при граничных условиях
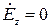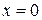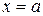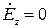для 
, 
,
для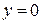 
, 
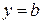. (41)
Решение уравнения (16) будет иметь такой же вид, как и решение уравнения (15), так как по форме эти уравнения одинаковы. Следовательно,
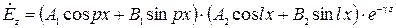(42)
и, аналогично,
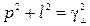и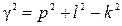 
.
При учете граничных условий (41) получим
; 
; 
; 
.
; 
; 
; 
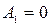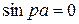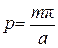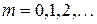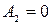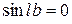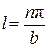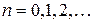. (43)
Также как и для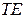 
-полей, волна будет бегущей, если выполняется условие (29). Учитывая это, а также условия (43), из уравнения (42) имеем
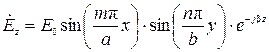, (44)
где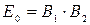 
.
Подставляя значение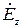 
в уравнения (19) и (20), получим выражения для комплексных амплитуд остальных составляющих векторов электромагнитного поля поперечно-магнитных (
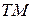или 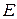) волн в прямоугольном волноводе.
Как и поля поперечно-электрического типа, в прямоугольном волноводе могут существовать бесчисленное множество полей поперечно-магнитного типа, определяемые значениями чисел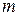 
и 
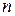. Поля поперечно-магнитного типа обозначаются символами 
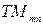или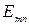 
. Значения чисел 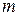и 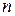не могут быть равными нулю, так как при этом составляющие векторов поля обращаются в нуль. Простейшим типом колебаний поперечно-магнитных волн является волна типа 
(
).
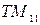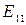Поскольку значения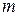 
и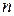 
для поперечно-магнитных и поперечно-электрических волн одни и те же (за исключением 
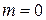и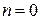 
), то критические частоты, критические длины волн, фазовые скорости и другие характеристики поперечно-магнитных волн различных типов могут быть рассчитаны по тем же формулам, что и соответствующие характеристики поперечно-электрических волн. Только характеристическое сопротивление волновода в случае поперечно-магнитной волны 
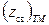будет отличаться от 
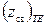и определяться выражением
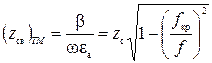. (45)
Мощность, передаваемая через поперечное сечение волновода волной 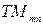, также будет определяться выражением (39).
Проведенный выше анализ полей различных типов указывает, что все возможные типы волн в прямоугольном волноводе исчерпываются полями, описываемые выражениями (33) при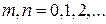 
и (45) при 
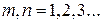. Эти поля называются собственными полями или собственными волнами прямоугольного волновода. Отсюда следует, что электромагнитное поле, возбуждаемое в волноводе произвольной системой источников, всегда может быть представлено в виде совокупности собственных волн.
В приложении Б приведена структура электромагнитных полей некоторых простейших типов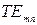 
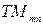- и -волн в прямоугольном волноводе.
