Метод Мора

Лекция 2.3. определение перемещений в упругих системах. Метод Мора. Способ Верещагина.

Метод Мора

Рассмотрим произвольную плоскую стержневую систему, нагруженную заданными силами 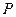(рис. 2.3.1). Усилия в произвольном сечении обозначим через 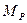, , 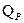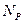. Пусть требуется определить перемещение любой точки 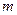системы по направлению .

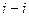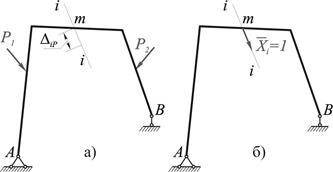
Рис.2.3.1

Введем вспомогательное состояние, представляющее собой заданную систему, нагруженную лишь одной единичной силой 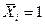, приложенной в той же точке 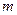и по тому же направлению, по которому надлежит разыскать перемещение 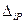. Усилия в произвольном сечении вспомогательного состояния, вызванные действием единичной силы 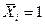, обозначим через , , .

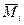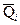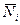Применим начало возможных перемещений для вспомогательного состояния, принимая в качестве возможных действительные перемещения заданной системы.

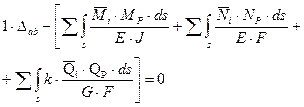(2.3.1)

или

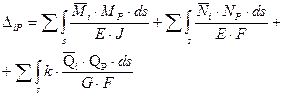(2.3.2)

Полученное выражение является общей формулой для упругого перемещения плоской стержневой системы.

В общем действии сил формула для перемещения содержит шесть слагаемых:

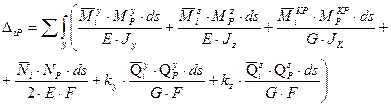(2.3.3)

Формулы (2.3.2) и (2.3.3) впервые были получены Мором. Определение перемещение по этим формулам часто называют методом Мора.

В большинстве случаев при определении перемещений в балках, рамах и арках можно пренебречь влиянием продольных деформаций сдвига, учитывая лишь перемещения, которые вызываются изгибом и кручением. Тогда формула (2.3.2) для плоской системы принимает вид

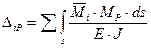. (2.3.4)

При пространственном нагружении, согласно (2.3.3),

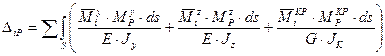(2.3.5)

Если рассчитываются шарнирные фермы, образованные прямыми стержнями, то в формуле Мора сохраняется только слагаемое, содержащее продольную силу:

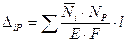(2.3.6)

Формула (2.3.6) носит название формулы Максвелла.

Рассмотрим пример определения перемещений по методу Мора. Пусть требуется определить прогиб посредине пролета и угол поворота на опоре шарнирно опертой балки постоянного поперечного сечения (рис 2.3.2, а), нагруженной равномерно распределенной нагрузкой интенсивностью 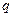. При определении перемещений придерживаются следующего порядка:

1. Строят вспомогательную систему, которую нагружают единичной нагрузкой в точке, где требуется определить перемещение. Определяя линейные перемещения, в заданном направлении прикладывают единичную силу, определяя угловые перемещения, - единичный момент.

В нашем случае, для определения прогиба посредине балки строим вспомогательную систему (рис. 2.3.2, б) с сосредоточенной силой 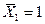, приложенной посредине балки, а для определения угла поворота опорного сечения - вспомогательную систему (рис. 2.3.2, в) с моментом 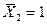, приложенным в опорном сечении.

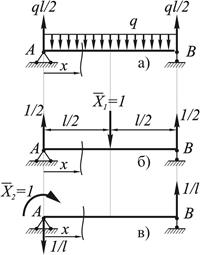
Рис. 2.3.2

2. Для каждого участка системы выписывают выражения силовых факторов в произвольном сечении заданной (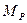, , 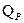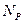) и вспомогательной (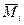, , 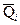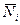) систем.

В произвольном сечении первого участка балки:

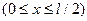
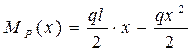
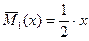
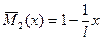
В произвольном сечении второго участка

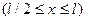
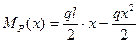
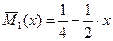
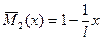
3. Вычисляют интегралы Мора (по участкам в пределах всей системы).

Прогиб посредине балки

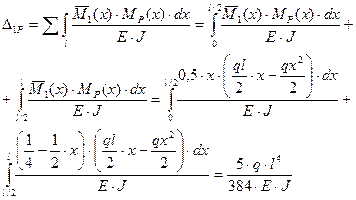
Угол поворота опорного сечения

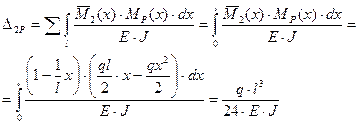
4. Если вычисленное перемещение имеет положительный знак, то это означает, что его направление совпадает с направлением единичной силы. Отрицательный знак указывает на то, что действительное направление искомого перемещения противоположно направлению единичной силы.

Поскольку 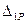и 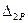получились положительными, их направления соответствуют единичным нагрузкам.