Вычисление интегралов Мора существенно можно упростить, если одна из эпюр прямолинейна. Такое условие всегда выполняется для систем, состоящих из прямых брусьев, так как при этом от единичной нагрузки всегда ограничены прямыми линиями.
Вычислим интеграл 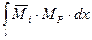 для случая, когда эпюра от заданной нагрузки имеет произвольное очертание, а от единичной нагрузки – прямолинейна (рис. 2.3.3).
для случая, когда эпюра от заданной нагрузки имеет произвольное очертание, а от единичной нагрузки – прямолинейна (рис. 2.3.3).
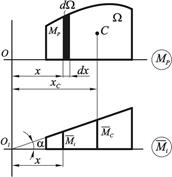
Рис. 2.3.3
Обозначим через 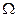 площадь эпюры
площадь эпюры 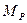 ;
; 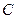 - ее центр тяжести,
- ее центр тяжести,  - ордината эпюры от единичной нагрузки под центром тяжести эпюры
- ордината эпюры от единичной нагрузки под центром тяжести эпюры 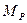 . Очевидно, что
. Очевидно, что 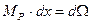 представляет собой дифференциал площади эпюры
представляет собой дифференциал площади эпюры 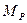 , а
, а
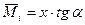 .
.
Тогда искомый интеграл
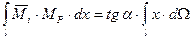 . (2.3.7)
. (2.3.7)
Интеграл в правой части равенства (2.3.7) представляет собой статический момент площади эпюры 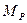 относительно оси
относительно оси 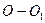
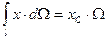 ,
,
где 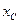 - абсцисса центра тяжести эпюры
- абсцисса центра тяжести эпюры 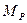 .
.
С учетом того, что
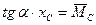 получим
получим
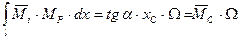 (2.3.8)
(2.3.8)
Следовательно, интеграл Мора равен произведению площади эпюры от внешней нагрузки на ординату прямолинейной эпюры от единичной нагрузки, расположенную под центром тяжести эпюры от заданной нагрузки.
Общая формула перемещений для систем из прямолинейных элементов принимает вид
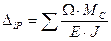 (2.3.9)
(2.3.9)
Описанный графоаналитический способ вычисления интеграла Мора впервые был предложен студентом А. Н. Верещагиным и носит название способа Верещагина.
Вычисление интеграла Мора способом Верещагина проводят по участкам, на каждом из которых эпюра от единичной нагрузки должна быть прямолинейной (рис. 2.3.4).
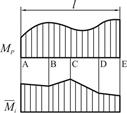
Рис. 2.2.4
Если эпюра 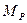 имеет сложный вид, то ее нужно разбить на простые фигуры (рис. 2.3.5), для которых легко определить площадь и положение центра тяжести. При этом каждую из площадей умножают на ординату единичной эпюры под центром тяжести соответствующей площади. Ординаты в этом случае удобно обозначать вместо
имеет сложный вид, то ее нужно разбить на простые фигуры (рис. 2.3.5), для которых легко определить площадь и положение центра тяжести. При этом каждую из площадей умножают на ординату единичной эпюры под центром тяжести соответствующей площади. Ординаты в этом случае удобно обозначать вместо 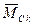 буквами
буквами 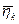 .
.
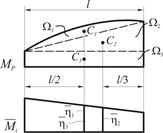
Рис. 2.3.5
Таким образом
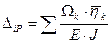 (2.3.10)
(2.3.10)
При учете крутящих моментов в общем случае нагружения знаменатель формулы (2.3.9) в соответствующем члене содержит жесткость на кручение 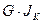 .
.
Если эпюры противоположны по знаку, то результат умножения эпюр имеет знак «минус».
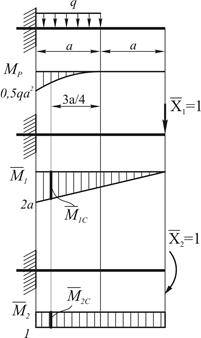 Рис. 2.3.6 Рис. 2.3.6 | Определим прогиб и угол поворота свободного конца консольной балки, нагруженной распределенной нагрузкой 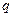 . На рис. 2.2.6 показаны эпюры . На рис. 2.2.6 показаны эпюры 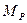 от внешней нагрузки, от внешней нагрузки, 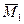 от единичной нагрузки от единичной нагрузки 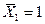 , приложенной в месте определения прогиба, , приложенной в месте определения прогиба, 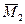 от единичной нагрузки от единичной нагрузки 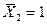 приложенной в месте определения угла поворота сечения. Площадь параболы под участком с распределенной нагрузкой приложенной в месте определения угла поворота сечения. Площадь параболы под участком с распределенной нагрузкой 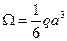 |
Центр тяжести этой площади находится на расстоянии 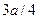 от начала распределенной нагрузки.
от начала распределенной нагрузки.
Ордината вспомогательной эпюры, расположенная под центром тяжести эпюры 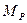 от внешней нагрузки
от внешней нагрузки  .
.
Прогиб свободного конца балки
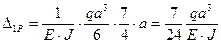
Ордината вспомогательной эпюры 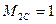
Угол поворота крайнего правого сечения
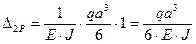
 2015-09-06
2015-09-06 1625
1625







