Пусть кривая L задана в полярной системе координат:
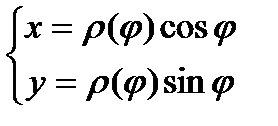
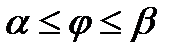 ,тогда L=
,тогда L= 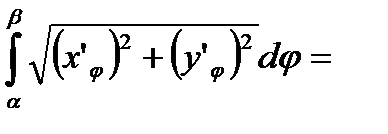
= 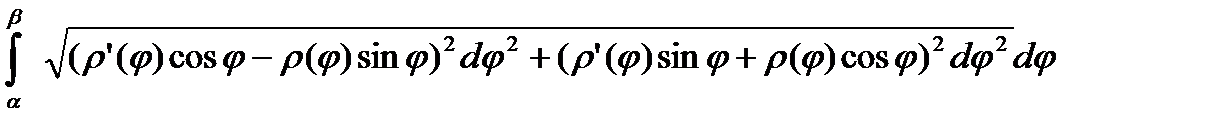 =
=
= 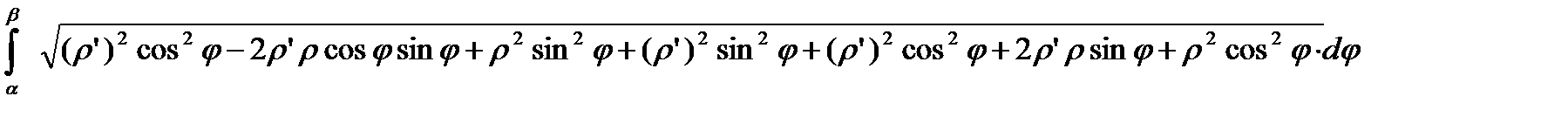 =
=
= 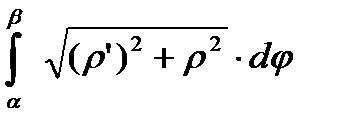 .
.
Длина дуги кривой в полярной системе координат L= 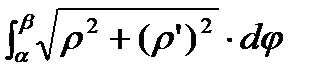 .
.
Пример: Вычислить длину кардиоиды 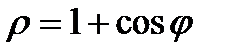 . В силу симметричности кривой вычислим ½ длины. ½L=
. В силу симметричности кривой вычислим ½ длины. ½L= 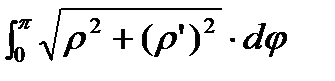
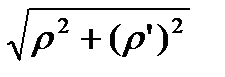 =
= 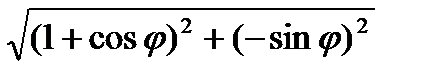 =
=
= 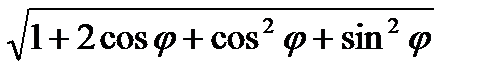 =
= 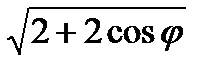 =
= 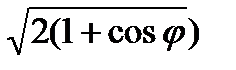 =
= 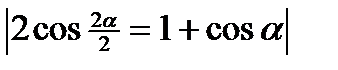 =
=
= 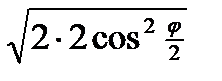 =
= 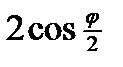
½L= 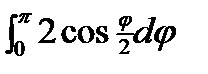 =
= 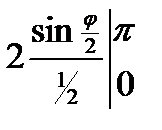 =4(1-0)=4 ÞL=4∙2=8
=4(1-0)=4 ÞL=4∙2=8
Дифференциал дуги.
Пусть в формуле L = 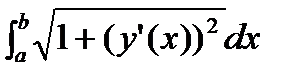 для длины дуги нижняя граница остается постоянной, а верхняя граница изменяется. Чтобы подчеркнуть это, обозначим верхнюю границу буквой x, а переменную интегрирования – буквой t. Учтем, что длина дуги L есть функция верхней границы, тогда получим:
для длины дуги нижняя граница остается постоянной, а верхняя граница изменяется. Чтобы подчеркнуть это, обозначим верхнюю границу буквой x, а переменную интегрирования – буквой t. Учтем, что длина дуги L есть функция верхней границы, тогда получим:
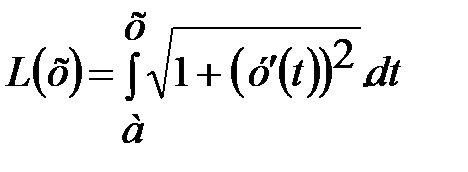
Согласно теореме о производной интеграла по верхней границе эта функция дифференцируема, и ее производная находится по формуле:


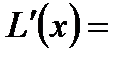
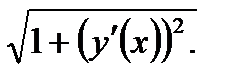
Отсюда дифференциал дуги  dL
dL 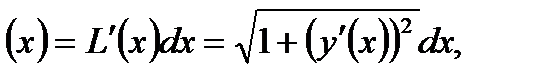
 или, в сокращенной записи, dL =
или, в сокращенной записи, dL = 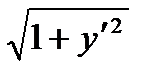 dx. Так как
dx. Так как 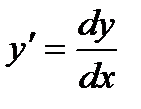
 , то dL =
, то dL = 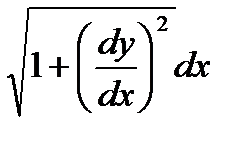 , или dL =
, или dL = 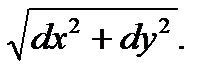
Учитывая полученный результат и то, что дифференциал функции равен приращению ординаты касательной, приходим к следующему геометрическому смыслу дифференциала дуги: дифференциал дуги dL равен длине отрезка касательной от точки касания с абсциссой x до точки с абсциссой x+dx.
Вопросы для самоконтроля:
1.Запишите формулу для вычисления длины дуги кривой, заданной в декартовой системе координат.
2.Запишите формулу для вычисления длины дуги, заданной параметрически.
3.Запишите формулу для вычисления длины дуги, заданной в полярной системе координат.
4.Каков геометрический смысл дифференциала дуги?
Задачи для самостоятельного решения:
1.Найти длину дуги параболы y= 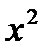 отx=0 доx=1.
отx=0 доx=1.
2. Найти длину дуги кривой x= 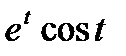 , y=
, y= 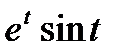 от t=0 до t=1.
от t=0 до t=1.
3.Найти длину дуги кардиоиды r=2 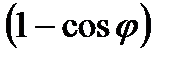 .
.
Пример 1. Найти длину линии  от точки
от точки 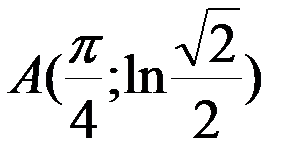
до точки 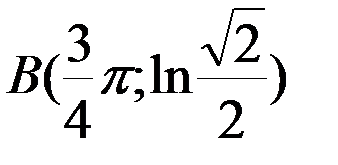 .
.
Решение: Линия задана в декартовой системе координат. Очевидно, что 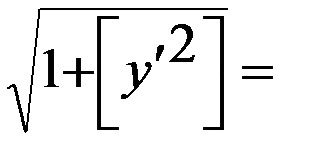
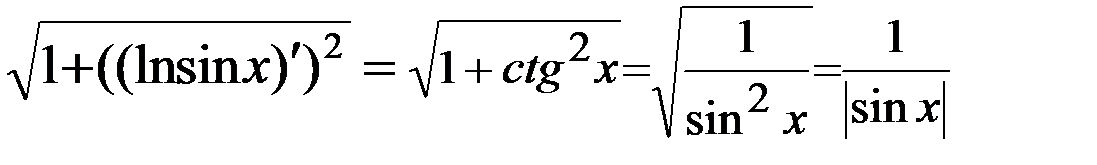 .
.
Так как на рассматриваемом промежутке 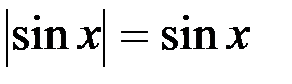 , то
, то
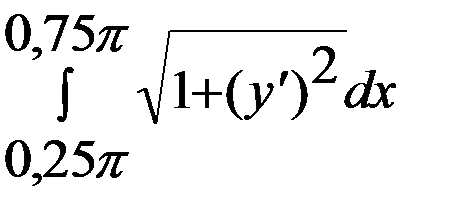 =
= 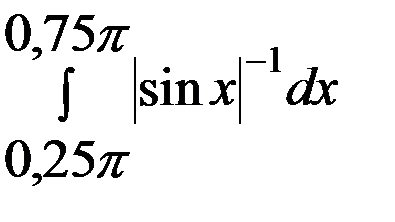 =
= 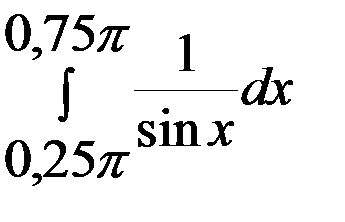 =
=
= 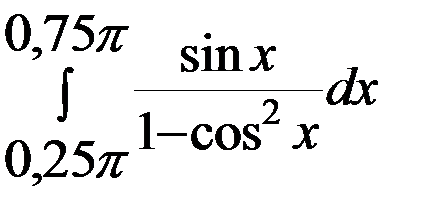 =
= 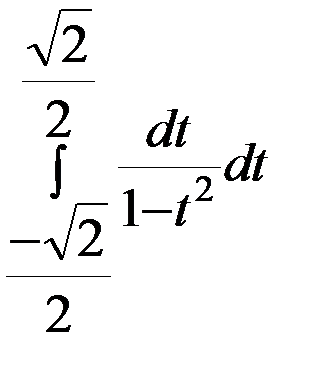 =
= 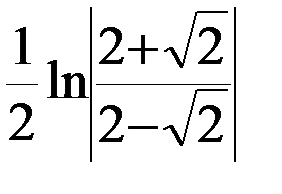
Отметим, что при вычислении интеграла мы воспользовались заменой:
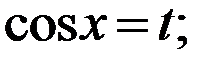
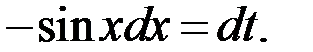
Пример 2. Найти длину кривой 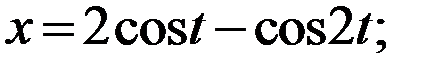
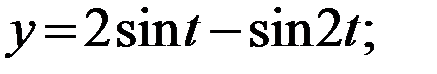
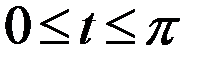 .
.
Решение: Кривая задана параметрически. Легко видеть, что
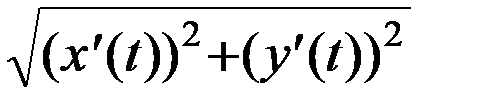 =
= 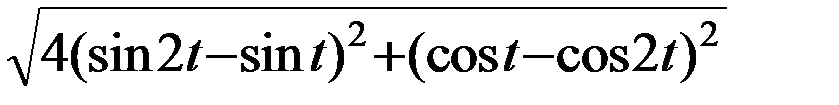 =
=
= 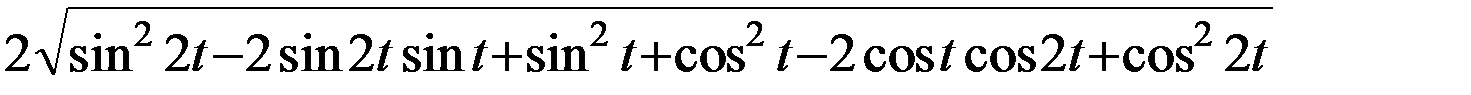 =
=
= 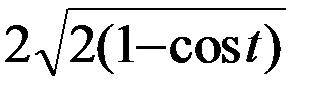 =
= 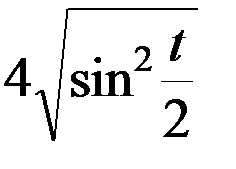 =
= 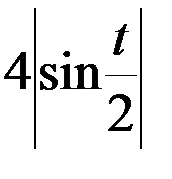 .
.
Так как на промежутке 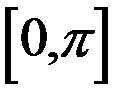 выполняется равенство
выполняется равенство 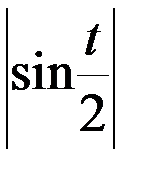 =
= 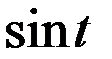 , то
, то
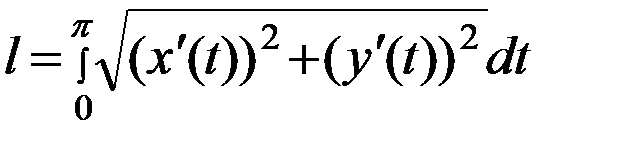 =
= 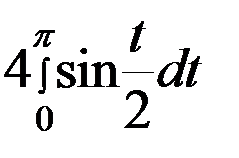 =
= 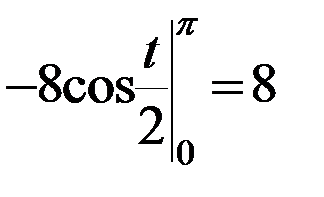
Пример 3.
Найти длину дуги кардиоиды r=a(1+cos 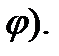
Решение: Кардиоида симметрична относительно полярной оси. Изменяя полярный угол 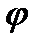 от 0 до
от 0 до 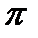 , мы получим половину длины кардиоиды:
, мы получим половину длины кардиоиды:
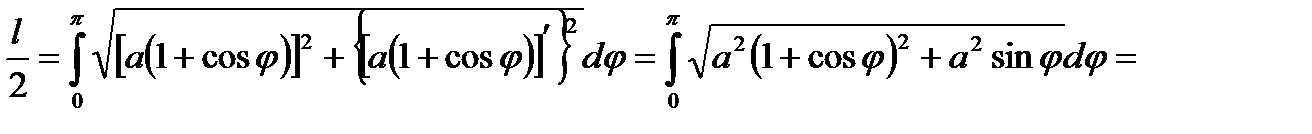
= a 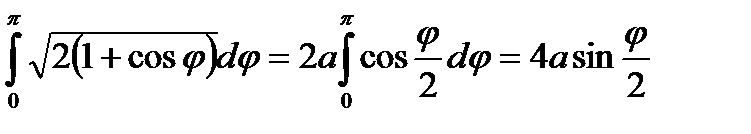 │
│ 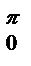 =4asin
=4asin 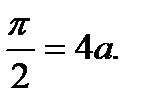
Вся длина кардиоиды l=2 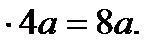
Можно показать, что для длины дуги пространственной кривой, заданной уравнениями x=x(t), y=y(t), z=z(t), 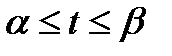 , имеет место следующая формула:
, имеет место следующая формула:
l = 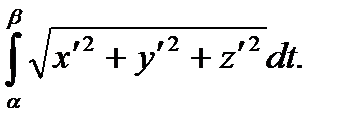
 2015-09-06
2015-09-06 6043
6043







