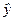Решение типовых задач

Задача 1. Методом случайной повторной выборки было взято для проверки на вес 200 шт. деталей. В результате был установлен средний вес детали - 30 г при среднеквадратическом отклонении равном 4 г. С вероятностью 0,954 требуется определить предел, в котором находится средний вес детали в генеральной совокупности.

Решение.

Предельная ошибка средней при собственно-случайном отборе (повторная выборка) определится по формуле:

.

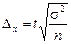Нам известно, что t = 2 (т.к. P = 0.954); 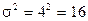; n = 200, тогда

.

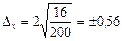Следовательно, с вероятностью 0,954 можно утверждать, что средний вес детали в генеральной совокупности будет находиться в пределах:

.

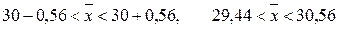Задача 2. Был проведен учет городского населения города А методом случайного бесповторного отбора. Из общей численности населения 500 тыс. человек было отобрано 500 тыс. и установлено, что 15% имеют возраст старше 60 лет. С вероятностью 0,683 определить предел, в котором находится доля жителей города А в возрасте старше 60 лет.

Решение.

Предельная ошибка доли при собственно-случайном бесповторном отборе определится как

.

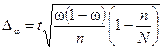Здесь 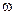= 0.15; 1- 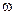= 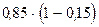; n = 50; N = 500; t = 1 (P = 0.683), тогда подставляя эти данные в формулу получим:

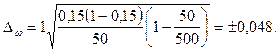
Следовательно, с вероятностью 0,683 можно утверждать, что доля жителей старше 60 лет находится в пределах:

0,15 - 0,048 < P < 0,15 + 0,048; или 10,2% < P < 19,8%.

Задача 3. Проведена 10%-ная типическая выборка пропорциональна численности отобранных групп (табл. 6.3).

Таблица 6.3

Группировка рабочих разных профессий по степени выполнения норм выработки

Группы рабочих	Число рабочих	Среднее выполнение норм, %
Токари
Слесари
Фрезеровщики

Требуется с вероятностью 0,954 определить пределы, в которых находится средний процент выполнения норм рабочими завода в целом. Выборка бесповторная.

Решение: Вычислим общий средний процент выполнения норм выработки:

.

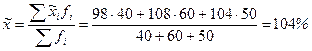Далее определим среднюю из групповых дисперсий:

.

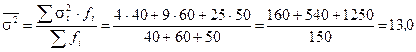Рассчитаем предельную ошибку выработки для типического отбора:

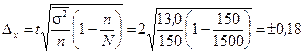. (N = 1500, т.к. выборка 10%-ная).

Таким образом, с вероятностью 0,954 можно утверждать, что средний процент выполнения норм рабочими завода в целом находится в пределах:

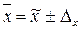или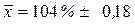

т.е. он не меньше 103,82% и не больше 104,18%.

Задача 4. Для определения средней урожайности сахарной свеклы в области проведена 20%-ная серийная бесповторная выборка, в которую вошло 5 районов из 25. Средняя урожайность по каждому отобранному району составила: 250, 260, 275, 280, 300 ц/га. Определить с вероятностью 0,954 пределы, в которых будет находиться средняя урожайность сахарной свеклы по области.

Решение. Найдем общую среднюю:

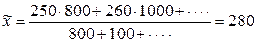ц/га.

Определим межсерийную дисперсию по формуле:

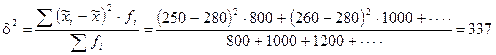ц/га.

Рассчитаем предельную ошибку выборки при серийном бесповторном отборе:

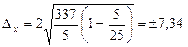ц/га.

Следовательно, с вероятностью 0,954 можно утверждать, что средняя урожайность сахарной свеклы в области будет находиться в пределах от 272,66 до 287,34 ц/га.

Задача 5. Предполагается, что партия деталей содержит 8 % брака. Определить необходимый объем выборки, чтобы с вероятностью 0,954 можно было установить долю брака с погрешностью не более 2%. Исследуемая партия содержит 5000 деталей.

Решение. По условию задачи t = 2, доля бракованных деталей 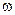= 0,08,

1- 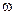= 0,92. Предельная ошибка доли по условию равна 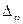= 0,02, а N = 5000.

Подставляем эти данные в формулу и получим:

.

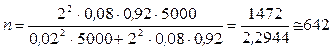Чтобы с вероятностью 0,954 можно было утверждать, что предельная ошибка доли брака не превысит 2%, необходимо из 5000 деталей отобрать 642.

Задача 6.

Что произойдет с предельной ошибкой выборки, если:

а) дисперсия уменьшится в 4 раза;

б) численность выборки увеличить в 9 раз;

в) вероятность исчисления изменится с 0,683 до 0,997.

Решение.

Из формулы для расчета предельной ошибки выборки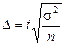

видно, что она:

а) прямо пропорциональна корню квадратному из дисперсии. Следовательно, если дисперсия уменьшится в 4 раза, то предельная ошибка уменьшится в 2 раза;

б) обратно пропорциональна корню квадратному из численности выборки. Следовательно, если объем выборки увеличится в 9 раз, то предельная ошибка уменьшится в 3 раза;

в) прямо пропорциональна вероятности исчисления, т.е. при увеличении Р с 0,683 (t = 1) до 0,997 (t = 3) ошибка увеличится в 3 раза.

СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ СВЯЗИ

Виды и формы взаимосвязи между явлениями

Одной из важнейших задач статистики является изучение, измерение и количественное выражение взаимосвязи между явлениями общественной жизни, установленной на основе качественного анализа.

Различают два вида связей: функциональную и корреляционную, обусловленные двумя типами закономерностей: динамическими и статистическими.

Для явлений, в которых проявляются динамические закономерности, характерна жесткая, механическая причинность, которая может быть выражена в виде уравнения, четкой зависимости и т.д. Такая зависимость называется функциональной. При функциональной связи каждому значению одной величины (аргумента) соответствует одно или несколько вполне определенных значений другой величины (функции).

В общественных процессах, в которых проявляются статистические закономерности, нет строгой зависимости между причиной и результатом и обычно не представляется возможным выявить строгую зависимость.

Связь, при которой каждому значению аргумента соответствует не одно, а несколько значений функции и между аргументом и функциями нельзя установить строгой зависимости называется корреляционной. Корреляционная зависимость проявляется только в средних величинах и выражает числовое соотношение между ними в виде тенденции к возрастанию или убыванию одной переменной величины при возрастании или убывании другой.

По направлению различают прямую и обратную связи.

По аналитическому выражению корреляционная связь может быть прямолинейной и криволинейной.

Основные приемы изучения взаимосвязей

а) Метод параллельных рядов. Чтобы установить связь между явлениями достаточно расположить полученные в результате сводки и обработки материалы в виде параллельных рядов и сопоставить их между собой.

б) Балансовый метод. Для характеристики взаимосвязи между явлениями в статистике широко применяется балансовый метод. Сущность его заключается в том, что данные взаимосвязанных показателей изображаются в виде таблицы и располагаются таким образом, чтобы итоги между отдельными частями были равны, т.е. чтобы был баланс. Балансовый метод используется для характеристики взаимосвязи между производством и распределением продуктов, денежными доходами и расходами населения и т.д.

в) Метод аналитических группировок. При наличии массовых статистических данных для изучения и измерения взаимосвязей социально-экономических явлений широко пользуются методом аналитических группировок. Аналитические группировки позволяют установить наличие связи между двумя и более признаками и ее направление. Метод группировок сочетается с методом средних и относительных величин.

г) Дисперсионный анализ. Аналитические группировки при всей своей значимости не дают количественного выражения тесноты связи между признаками. Эта задача решается при помощи дисперсионного и корреляционного анализов.

Дисперсионный анализ дает, прежде всего, возможность определить роль систематической и случайной вариаций в общей вариации и, следовательно, установить роль изучаемого фактора в изменении результативного признака. Для этого пользуются правилом сложения дисперсий.

Корреляционный анализ

Определение формы связи

Изучение взаимосвязей между признаками статистической совокупности заключается в определении формы и количественной характеристики связи, а также степени тесноты связи. Корреляционный анализ и решает эти две основные задачи.

Первая задача заключается в определении формы связи, т.е. в установлении математической формы, в которой выражается данная связь.

Предварительный этап при установлении формы связи заключается в теоретическом анализе изучаемого явления, а также в представлении искомой связи графически. График, построенный по исходным данным, позволяет приблизительно определить: есть ли какая-то связь между явлениями; ее направление (прямая или обратная); примерную тесноту связи (естественно, что при графическом анализе используются только две переменные).

Применение методов корреляционного анализа дает возможность выражать связь между признаками аналитически - в виде уравнения - и придавать ей количественное выражение.

Другими словами необходимо найти зависимость вида y = f (x), причем в качестве функции f (x) могут быть:

полином 1-го порядка -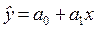

полином 2-го порядка -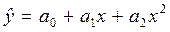

степенная функция -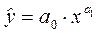

гиперболическая функция -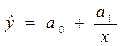

(могут быть использованы и другие виды функций).

Неизвестные параметры функций (аналитических уравнений связи) находятся методом наименьших квадратов, сущность которого в следующем: сумма квадратов отклонений фактических данных от выровненных должна быть наименьшей (см. рисунок):

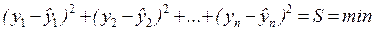
или

y

x

Ù

y

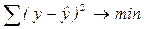
Отклонение фактических уровней от выровненных

Измерение тесноты связи

При изучении корреляционной связи важно выяснить не только форму, но и тесноту связи между факторным и результативным признаком. Для этого (при прямолинейной связи) рассчитывается показатель, называемый парным линейным коэффициентом корреляции 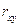, вычисляемый по формуле

.

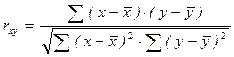Коэффициент корреляции принимает значение от -1 до +1, причем если 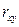> 0, то корреляция прямая, если 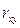< 0, то корреляция обратная, а если 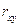= 0, то корреляция отсутствует полностью.

В зависимости от того, насколько 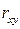приближается к единице, различают связь слабую, умеренную, заметную, высокую, тесную и весьма тесную.

Коэффициент корреляции может быть исчислен и по следующей формуле ,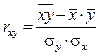

где 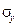- среднее квадратическое отклонение результативного признака;

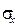- среднее квадратическое отклонение факторного признака.

Зная линейный коэффициент корреляции, можно определить и параметры уравнения регрессии вида 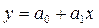потому что:

.

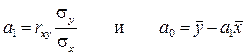Коэффициент корреляции 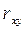применяется только в тех случаях, когда между явлениями существует прямолинейная связь.

Если же связь криволинейная, то пользуются коэффициентом корреляции, вычисляемым по формуле:

,

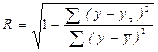где y - исходные значения результативного показателя;

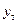- теоретические значения;

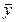- среднее значение y.

Имея среднее значение дисперсий, коэффициент корреляции можно вычислить как:

,

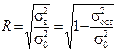где 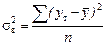- факторная (межгрупповая) дисперсия или дисперсия воспроизводимости;

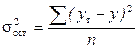- случайная (средняя из внутригрупповых) дисперсия или остаточная дисперсия; 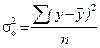- общая дисперсия.

Коэффициент корреляции по своему абсолютному значению находится в пределах от 0 до 1.

Если коэффициент корреляции возвести в квадрат и выразить в процентах, получим показатель, называемый коэффициентом детерминации:

D =  R ^{2 ·} 100%.

Он показывает, на сколько процентов изменение результативного фактора зависит от изменения факторного признака. Коэффициент детерминации является наиболее конкретным показателем, так как он отвечает на вопрос о том, какая доля в общем результате зависит от фактора, положенного в основании группировки.

Множественная корреляция

Определение формы и тесноты связи между тремя и более параметрами называется множественной корреляцией. При множественной корреляции определение формы связи аналогично определению формы связи при парной корреляции, а само уравнение регрессии ищется в виде (как правило):

.

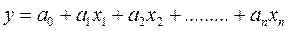При определении тесноты связи есть свои особенности. Теснота связи измеряется множественным коэффициентом корреляции, вид которого аналогичен коэффициенту корреляции при парной связи:

.

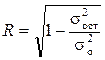Если изучается взаимодействие только трех факторов y = f (x, z), то коэффициент множественной корреляции можно определить по формуле:

,

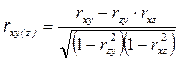где 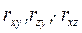- парные коэффициенты корреляции.

Множественный коэффициент корреляции находится в пределах от 0 до 1.

Множественный коэффициент детерминации, равный квадрату R, выраженному в процентах, характеризует долю вариации результативного признака Y под воздействием всех изучаемых факторных признаков.

Поскольку факторные признаки действуют не изолировано, а по взаимосвязи, то может возникнуть задача определения тесноты связи между результативным признаком и одним из факторных при постоянных значениях прочих факторов. Она решается при помощи частных коэффициентов корреляции. Например, при линейной связи y = f (x, z) частный коэффициент корреляции между x и y при постоянном z вычисляется по следующей формуле:

.

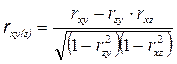Частный коэффициент корреляции при изучении зависимости Y от Z при постоянном Х определяется по формуле:

.

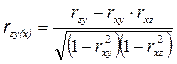Парные коэффициенты корреляции, как правило, выше частных. Это объясняется тем, что факторы взаимно коррелируют между собой.

При значительном количестве факторов частный коэффициент корреляции можно получить по формуле:

,

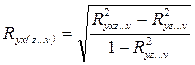где 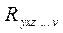- коэффициент множественной корреляции; 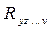- коэффициент множественной корреляции результативного фактора (y) со всеми за исключением исследуемого.

Простейшие методы измерения тесноты связи

Измерение тесноты связи между факторами с помощью корреляционно-регрессионного и дисперсионного анализов сопряжено с большими вычислительными трудностями. Для ориентировочной оценки степени тесноты связи существуют приближённые методы, не требующие трудоемких расчетов. К ним относятся: коэффициент корреляции знаков Фехнера, коэффициент корреляции рангов, коэффициент ассоциации и коэффициент взаимной сопряженности.

Коэффициент корреляции знаков.

Основан на сопоставлении знаков отклонений от средней и подсчете числа случаев совпадения и несовпадения знаков. Коэффициент корреляции знаков определяется по формуле:

,

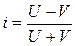где U - число пар с одинаковыми знаками отклонений x и y от 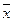и ;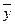

V - число пар с разными знаками отклонений x и y от 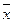и .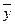

Коэффициент корреляции знаков колеблется от -1 до +1. Этот показатель исчисляется очень просто, но именно в силу этого он не очень точен.

Коэффициент корреляции рангов.

Этот показатель вычисляется не по первичным данным, а по рангам (порядковым номерам), которые присваиваются всем значениям изучаемых признаков, расположенным в порядке их возрастания. Если значения признака совпадают, то определяется средний ранг путем деления суммы рангов на число совпадающих значений. Коэффициент корреляции рангов определяется по формуле:

,

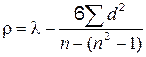где 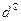- квадрат разности рангов для каждой единицы d = x - y.

Коэффициент корреляции рангов также колеблется в пределах от -1 до +1.

Коэффициент ассоциации.

Коэффициент ассоциации применяется для установления меры связи между двумя качественными альтернативными признаками.

Для его вычисления строится комбинационная 4-клеточная таблица:

а	б
с	д

которая выражает связь между двумя альтернативными явлениями.

Коэффициент ассоциации рассчитывается по формуле:

.

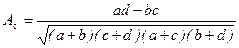Коэффициент ассоциации тоже колеблется в пределах от -1 до +1.

Коэффициент взаимной сопряженности

В тех случаях, когда требуется установить связь между качественными признаками, каждый из которых состоит из трех и более групп, применяется коэффициент взаимной сопряженности. Для определения степени тесноты связи вычисляется специальный показатель, который называется коэффициентом взаимной сопряженности.

Он определяется по формуле:

,

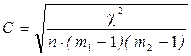где n - число единиц совокупности;

m ₁ и m ₂ - число групп по первому и второму признаку;

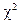- показатель абсолютной квадратичной сопряженности Пирсона.

Методика применения всех четырех коэффициентов показана при решении типовых задач.