Рівняння Ван-дер-Ваальса

Зі сказаного в § 8.1 ясно, що в першому наближенні молекули реального газу можна уподібнити абсолютно твердим кулькам з діаметром 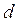, між якими діють лише сили притягання. Враховуючи кінцеві розміри молекул, ми, таким чином, беремо до уваги дію сил взаємного відштовхування між ними.

Така модель газу, прийнята голландським фізиком Я. Ван-дер-Ваальсом, дала йому можливість отримати рівняння стану реального газу, більш досконале, ніж рівняння Мендєлєєва–Клапейрона.

У рівнянні стану одного моля ідеального газу:

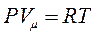(8.7)

Ван-дер-Ваальс урахував власний об’єм молекул газу шляхом заміни повного об’єму 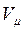посудини з газом на так званий „вільний” об’єм:

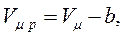(8.8)

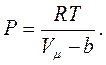де 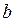– поправка Ван-дер-Ваальса, що залежить від власного об’єму молекул: 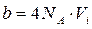[6]. Тут: 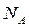– число Авогадро, 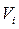– власний об’єм однієї молекули, який залежить від природи газу. Одиниця виміру цієї поправки в системі СІ 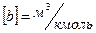. Враховуючи лише власний об’єм молекул і не враховуючи взаємодію між ними, на підставі рівнянь (8.7) та (8.8) отримаємо:

(8.9)

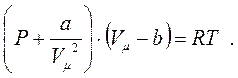Внаслідок притяжіння між молекулами тиск газу на стінки посудини зменшується на величину 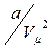[6]. Тут 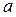– стала, що залежить від природи газу. Одиниця виміру 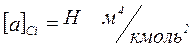.Враховуючи поправку на тиск, отримаємо:

(8.10)

Це і є рівняння стану одного моля реального газу.

Щоб отримати рівняння Ван-дер-Ваальса для довільної маси 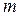реального газу, необхідно молярний об’єм газу 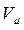визначити через об’єм 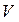всієї маси газу (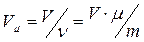, де 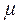– молярна маса газу) і ліву та праву частини рівняння (8.10) домножити на кількість молів. Після таких перетворень отримаємо:

(8.11)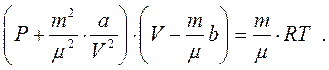

Це рівняння точніше узгоджується з результатами дослідів, ніж рівняння (8.1). Однак для дуже стиснених газів воно теж виявляється недостатньо вірним.

У випадку розріджених газів 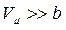, поправка на тиск 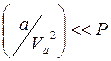і рівняння Ван-дер-Ваальса не відрізняється від рівняння Мендєлєєва–Клапейрона.