В классическом случае

Для описания движений атомов в молекуле в классической теории пользуются представлением смещения атомов в молекуле, при которых силы, возвращающие атомы в состояние равновесия, пропорциональны величинам смещений и направлены в сторону равновесного положения. Согласно законам механики, система в этом случае совершает гармонические колебания.

В качестве величин, определяющих смещение атомов в молекуле от равновесных положений, вводят n независимых параметров (колебательных координат) q ₁, q _2,,..., q_n, характеризующих изменения межъядерных расстояний и валентных углов по отношению к состоянию равновесия, т. е. q ₁ = r ₁ – r _{1 e}, q ₂ = r ₂ – r _2e,... q_n – q_ne, где r_e означает равновесное положение данного атома; значок n пробегает все колебательные степени свободы молекулы.

Кинетическая Т и потенциальная V энергии молекулы при малых колебаниях выражаются через колебательные координаты следующим образом

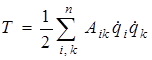, (4.1)

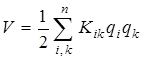, (4.2)

где 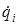и 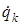– скорости движения атомов; q_i и q_k величины смещений i ^го и k -го атомов из положения равновесия; A_ik – величина, зависящая от масс колеблющихся атомов и их расположения в пространстве (кинематические коэффициенты); K_ik – квазиупругая постоянная, возникающая при изменении положения i -го и k -го – атомов; значки i и k независимо принимают значения от единицы до n (число колебательных степеней свободы). Величины А_ik являются симметричными по индексам, так как они служат коэффициентами перед численно равными величинами q_iq_k и q_kq_i

Для небольших смещений из положения равновесия потенциальную энергнию V можно разложить в степенной ряд по степеням свободы q_i

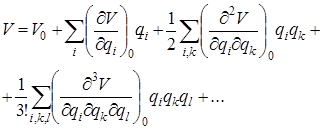(4.3)

Можно выбрать систему координат так, чтобы равновесное значение потенциальной энергии V ₀ равнялось нулю. тогда формула (4.3) значительно упростится. Кроме того, в состоянии равновесия все q_i и 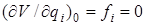, где f_i – квазиупругая сила, действующая на i -ю связь.

Для достаточно малых амплитуд колебаний можно пренебречь высшими членами разложения, в которые входят q в третьей, четвертой и высших степенях. После этого получим:

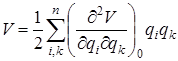, (4. 4)

что совпадает с формулой (4.2), если принять 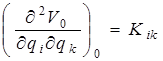(индексы i и k не равны друг другу и пробегают значения от i, k = 1 до п).

Уравнения движения Ньютона для многоатомной молекулы удобно записать в такой форме, в которую бы входили значения кинетической и потенциальной энергий. В этом случае необходимо записать функцию Лагранжа для молекулы, совершающей малые колебания, в виде

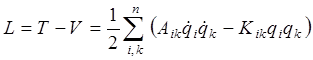, (4.5)

а затем записать уравнения движения в форме Ньютона, т. е.

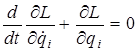
или

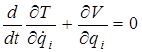, (4.6)

так как Т – функция только скоростей, а V – функция только координат. Подставив в (4. 6) значения кинетической и потенциальной энергии (4.1) и (4.2), получим следующее выражение:

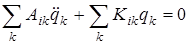. (4.7)

Формула (4.7) представляет собой систему n (i, = l, 2,..., n) линейных однородных дифференциальных уравнений с постоянными коэффициентами. Эта система в развернутом виде может быть записана следующим образом:

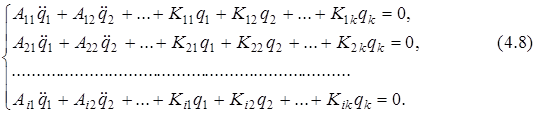
Соотношение (4.7) представляет собой систему n совместных дифференциальных уравнений второго порядка. Одно из возможных решений этой системы в гармоническом приближении ищем в виде

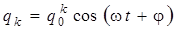, (4.9)

где q₀^k амплитуда k -го колебания; w – угловая частота; j – начальная фаза. Примем для простоты начальную фазу j = 0. Тогда подстановка равенства (4.9) в систему дифференциальных уравнений (4.8) позволяет получить систему алгебраических уравнений вида

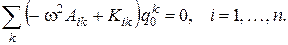. (4.10)

Это система однородных линейных алгебраических уравнений относительно n неизвестных амплитуд колебаний q_k ⁰. В развернутом виде эту систему можно записать следующим образом

,

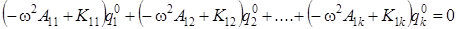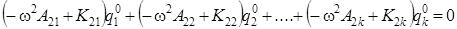, (4.11)

..............................,

.

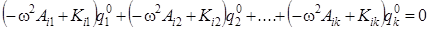Условием разрешимости системы (4.11) является равенство нулю определителя, составленного из коэффициентов при неизвестных амплитудах, т. е.

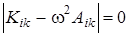. (4.12)

В развернутом виде этот определитель будет выглядеть так:

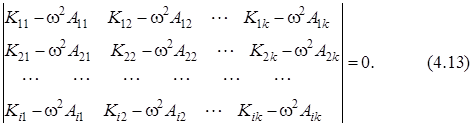
Уравнение (4.12) называется характеристическим. Оно в общем случае имеет n различных вещественных положительных корней 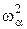(a = l, 2,..., n). Величины 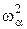, определяемые из этого уравнения, называются собственными частотами колебаний молекулы. Только для этих значений 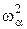в определителе (4.11) получают ненулевые значения 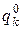. Определив одно из значений 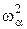, обращающих детерминант (4.12) в нуль, можно найти коэффициенты в уравнениях (4.11) перед неизвестными 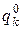. Это позволит получить решения системы (4.10) в виде 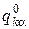, где индекс a указывает на соответствие с данным значением 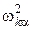. Однако система уравнений (4.10) не определяет однозначно 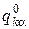, а только их отношения. Если принять значение одной из амплитуд колебаний за единицу (например, 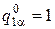), то мы получим набор значений амплитуд 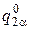, 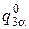и т. д. в условных единицах. Каждый корень определителя (4.12) соответствует набору амплитуд 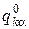и, следовательно, решению (4.10) исходных уравнений движения.

Если все частоты w_a найдены из корней определителя (4.12) (в предположении, что коэффициенты А_ik и К_ik известны), то из (2.10) можно рассчитать все коэффициенты 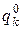(амплитуды колебаний).

Исследуем характер полученных решений. Из уравнения (4.9) следует, что каждый атом колеблется около своего положения равновесия по закону простого гармонического движения с амплитудой 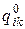, частотой w _k и фазой j_a.Частота и фаза, соответствующая данному решению векового уравнения, одинаковы для каждой координаты. Амплитуды смещений всех атомов, вообще говоря, различны. Мы видели, что каждому значению w_a векового определителя (4.12) соответствует свой набор амплитуд q_ik ⁰, характеризующий форму колебания.

Поскольку фаза и частота одинаковы, то все атомы достигают положения максимальных смещений в одно и то же время, и все атомы в одно и то же время проходят свои равновесные положения. Колебание, имеющее указанные характеристики, называется нормальным, а частота этого колебания – нормальной или фундаментальной.

Рассмотренные случаи решения системы уравнений (4.8) представляют собой частные решения. В общем случае изменение во времени каждой координаты q_k представляет собой совокупность одновременно происходящих гармонических колебаний с частотами ω₁, ω₂,... ω _k...

Изложенное выше справедливо в том случае, когда все частоты ω _k, допускаемые решением определителя (4.12), различны. Однако иногда, когда две или три частоты при решении уравнения (4.12) совпадают. В этом случае говорят о дважды или трижды вырожденном нормальном колебании. Картина колебаний атомов в молекуле при этом усложняется. Например, известно, что при сложении двух колебаний одинаковой частоты, но различных амплитуд и фаз результирующее движение может представлять собой возвратно-поступательное движение по прямой, по эллипсу, или движение по окружности.

4.3. Нормальные координаты и колебания.

Как было показано в п. 4.2, значения кинетической и потенциальной энергии колеблющейся молекулы были выражены через произведение скоростей 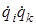и произведение q_iq_k координат. Однако, характеристическое уравнение 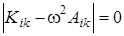и уравнение для нахождения амплитуд колебаний 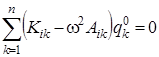можно упростить, если ввести такое преобразование координат, в результате которого все коэффициенты А_ik и K_ik обратятся в нуль для i ¹ k и останутся только те коэффициенты, для которых i = k. Можно показать математически, что такие координаты действительно существуют. Обозначим их через Q ₁, Q ₂,..., Q_n. Они определяются через координаты смещения q_k с помощью линейных уравнений

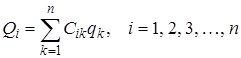, (4.14)

где C_ik – квадратная матрица, элементы которой подбираются так, чтобы в новых координатах кинетическая и потенциальная энергия имели вид

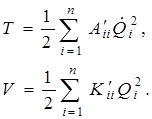(4.15)

В развернутом виде это может быть записано так:

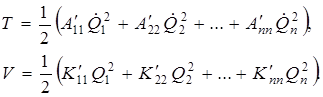(4.16)

Другими словами, в выражения для кинетической и потенциальной энергии в нормальных координатах входят только квадраты скоростей 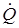и квадраты координат Q без перекрестных членов. С физической точки зрения это означает, что каждая такая координата изменяется независимо от других координат в процессе колебания.

Координаты Q_i, удовлетворяющие введенным выше условиям, называются нормальными координатами, а колебания молекулы представленные в этих координатах, называются нормальными (главными) колебаниями. Уравнение движения в этих координатах получится в виде, аналогичном (4.7), т. е. уравнение движения Ньютона в форме Лагранжа запишется в виде:

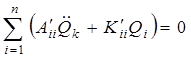. (4.17)

Итак, вместо (4.17) можно написать n уравнений по числу колебательных степеней свободы вида

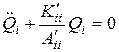
или

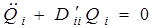(4.18)

где 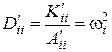– квадрат частоты собственных колебаний молекулы (i = 1, 2, 3,... n). Как видно, уравнение (4.18) описывает гармонические колебания системы атомов в молекуле. Решение уравнения (4.18), как следует из теории гармонического осциллятора, можно записать в виде

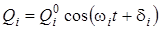, (4.19)

где w _i, – частота, совпадающая с одной из частот колебаний молекулы, Q_i ⁰ и d _i, – амплитуда и фаза этого колебания.

Таким образом, из уравнения (4.18) видим, что колебания молекулы в нормальных координатах – это гармонические колебания, которые совершаются с собственными частотами w _i. Уравнение движения в нормальных координатах для молекул распадается на n независимых уравнений гармонических колебаний. Каждая нормальная координата совершает независимое гармоническое колебание.

Матрицы кинетической и потенциальной энергии в нормальных координатах преобразуются к диагональной форме, а полная энергия

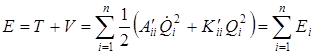(4.20)

равна сумме энергий E_i гармонических осцилляторов, колеблющихся по закону (4.19). Следовательно, любое колебательное движение системы (молекулы) может быть представлено как наложение нормальных колебаний с соответствующими амплитудами. Для наглядности формы колебаний часто изображают стрелками около атомов, передающими направления смещения при возбуждении одного из нормальных колебаний. Длина стрелки характеризует величину этих смещений.