Функции и параметры визуализации

Создадим графическую структуру решения системы дифференциальных уравнений для нескольких расчетных отклонений линии движения альфа-частицы от центра ядра атома, находящегося на ее пути.

> with(DEtools):ss:=DEplot({sys},{y(t),x(t)},t=0..7e-20,

[[x(0)=-a,D(x)(0)=V0x,y(0)=p,D(y)(0)=0],

[x(0)=-a,D(x)(0)=V0x,y(0)=p*8,D(y)(0)=0],

[x(0)=-a,D(x)(0)=V0x,y(0)=p*16,D(y)(0)=0],

[x(0)=-a,D(x)(0)=V0x,y(0)=p*24,D(y)(0)=0],

[x(0)=-a,D(x)(0)=V0x,y(0)=p*32,D(y)(0)=0],

[x(0)=-a,D(x)(0)=V0x,y(0)=-p*3,D(y)(0)=0],

[x(0)=-a,D(x)(0)=V0x,y(0)=-p*6,D(y)(0)=0],

[x(0)=-a,D(x)(0)=V0x,y(0)=-p*14,D(y)(0)=0],

[x(0)=-a,D(x)(0)=V0x,y(0)=-p*22,D(y)(0)=0],

[x(0)=-a,D(x)(0)=V0x,y(0)=-p*30,D(y)(0)=0],

[x(0)=-a,D(x)(0)=V0x,y(0)=-p*38,D(y)(0)=0]],

x(t)=-a..a,scene=[x(t),y(t)],stepsize=1e-21,linecolor=blue,labels=[Xм,Yм]):

Warning, the name translate has been redefined

Построим центр ядра (кружок со знаком "плюс") и траектории альфа-частиц:

> with(plottools):yy:=disk([0,0],2E-14,color=orange,thickness=2):

Warning, the names arrow and translate have been redefined

> ss2:=PLOT(TEXT([0,-0.3e-14],`+`),FONT(HELVETICA,OBLIQUE,14)):

Осталось построить совмещенный график траекторий движения альфа-частиц вблизи центра атома:

> with(plots):

Warning, the name arrow has been redefined

> display([ss,yy,ss2],title=`Рассеяние а-частиц`,titlefont=[TIMES,ROMAN,14]);

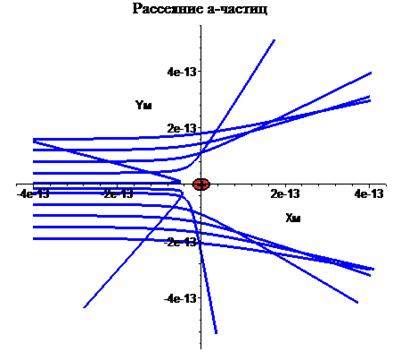
Моделирование движения альфа-частиц вблизи малого, но "массивного" ядра атома дает наглядное представление о математической и физической сути данного опыта. Надо лишь помнить, что нельзя нацеливать альфа-частицы прямо в центр ядра (т.е. прицельный параметр не может быть равен нулю). При уменьшении прицельного параметра формула Резерфорда начинает нарушаться (это означает, что частица начинает "чувствовать" поверхность ядра).