Функция распределения Максвелла имеет вид
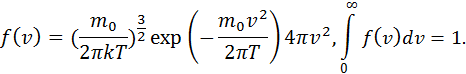
Из распределения молекул по скоростям Максвелла следует, что положение максимума функции распределения на оси скоростей и его значение имеют следующий вид
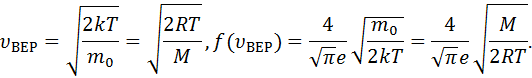
Здесь 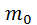 – масса молекулы и
– масса молекулы и 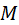 – молярная масса газа,
– молярная масса газа, 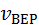 – скорость, при которой
– скорость, при которой 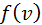 максимальна и равна
максимальна и равна 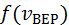 .
.
Примечание. Число молекул не влияет на распределение Максвелла.
При уменьшении М увеличивается 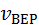 – максимум смещается вправо и уменьшается
– максимум смещается вправо и уменьшается 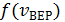 – высота максимума. Площадь под кривой не меняется и равна 1.
– высота максимума. Площадь под кривой не меняется и равна 1.
12. На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 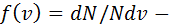 доля молекул, скорости которых заключены в интервале скоростей от
доля молекул, скорости которых заключены в интервале скоростей от 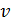 до
до 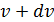 в расчете на единицу этого интервала:
в расчете на единицу этого интервала:
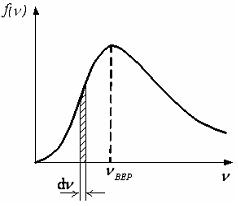
Для этой функции верными являются утверждения …
| – положение максимума кривой зависит не только от температуры, но и от природы газа (его молярной массы) | |||
| – при увеличении числа молекул площадь под кривой не изменяется | |||
| – с ростом температуры газа значение максимума функции увеличивается | |||
| – для газа с бόльшей молярной массой (при той же температуре) максимум функции расположен в области бόльших скоростей |
Решение
Функция Максвелла имеет вид
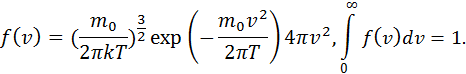
Из распределения молекул по скоростям Максвелла следует, что положение максимума функции распределения на оси скоростей и его значение имеют следующий вид
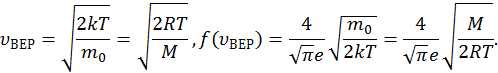
Здесь 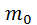 – масса молекулы и
– масса молекулы и 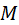 – молярная масса газа,
– молярная масса газа, 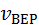 – скорость, при которой
– скорость, при которой 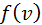 максимальна и равна
максимальна и равна 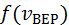 .
.
Положение максимума (значение 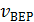 ) зависит и от температуры и от
) зависит и от температуры и от
природы газа (его молярной массы).
Площадь под кривой (вероятность) всегда равна 1.
При увеличении Т увеличивается 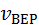 – максимум смещается вправо и уменьшается
– максимум смещается вправо и уменьшается 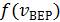 – высота (значение) максимума.
– высота (значение) максимума.
При увеличением М (молярной массы)уменьшается 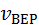 – максимум смещается влево (в область меньших скоростей) и увеличивается
– максимум смещается влево (в область меньших скоростей) и увеличивается 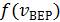 – высота максимума.
– высота максимума.
13. На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 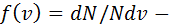 доля молекул, скорости которых заключены в интервале скоростей от
доля молекул, скорости которых заключены в интервале скоростей от 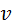 до
до 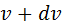 в расчете на единицу этого интервала:
в расчете на единицу этого интервала:

Для этой функции верными являются утверждения …
| – с увеличением температуры максимум кривой смещается вправо | |||
– площадь заштрихованной полоски равна доле молекул со скоростями
в интервале от 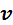 до до 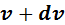
| |||
| – с ростом температуры значение максимума функции увеличивается | |||
| – с ростом температуры площадь под кривой увеличивается |
 2015-09-06
2015-09-06 545
545








