2015-09-06
2408
Предположим, что фирма производит n видов продуктов. Виды продуктов будем обозначать индексом j, а их количества - через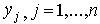 
. Технология производства каждого вида продукта требует использования ряда ресурсов в некоторых количествах. Двойными индексами 
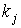обозначим виды ресурсов, используемых для выпуска продукта вида j. Пусть 
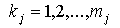.. Обозначим через 
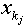- количества этих ресурсов, 
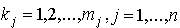. Следовательно, имеется всего 
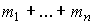видов ресурсов.
Введем в рассмотрение два вида векторов: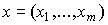 
- вектор затрат и 
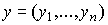- вектор выпуска. Положительный ортант
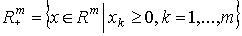
называется пространством затрат. Аналогично определяется пространство выпуска:
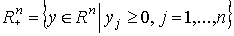
Для отражения реальных возможностей фирмы в математических моделях часто применяются более узкие множества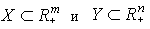 
.
Технологическая связь между затратами и выпуском описывается с помощью производственной функции.
Определение 4.1. Любая функция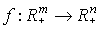 
, ставящая в соответствие каждому вектору затрат x вектор 
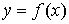максимального выпуска, который может быть получен при этих затратах, называется производственной функцией.
Производственная функция Кобба-Дугласа. Первый успешный опыт построения производственной функции, как уравнения регрессии на базе статистических данных, был получен американскими учеными - математиком Д. Коббом и экономистом П. Дугласом в 1928 году. Предложенная ими функция изначально имела вид:
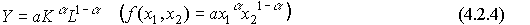
где Y - объем выпуска, K - величина производственных фондов (капитал), L - затраты труда,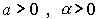 
- числовые параметры (масштабное число и показатель эластичности).
Для многофакторного производства функция Кобба-Дугласа имеет вид:
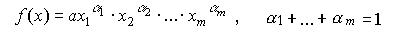
Для учета технического прогресса в функцию Кобба-Дугласа вводят специальный множитель (технического прогресса)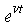 
, где t - параметр времени, 
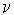- постоянное число, характеризующее темп развития. В результате функция принимает "динамический" вид:
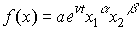
где не обязательно
Производственная функция CES (с постоянной эластичностью замещения) имеет вид:
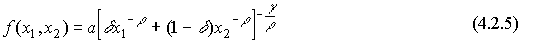
где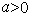 
- коэффициент шкалы, 
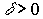- коэффициент распределения, 
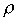- коэффициент замещения, 
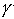- степень однородности. Если выполнены условия
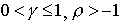
то функция (4.2.5) удовлетворяет неравенствам (4.2.2) и (4.2.3) (проверьте это самостоятельно). С учетом технического прогресса функция CES записывается:
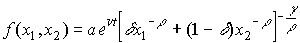
Название данной функции следует из того факта, что для нее эластичность замещения постоянна (см. §4.3).
Производственная функция с фиксированными пропорциями. Эта функция получается из (4.2.5) при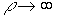 
и имеет вид:
Производственная функция затрат-выпуска (функция Леонтьева) получается из (4.2.6) при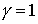 
:
Содержательно эта функция задает пропорцию, с помощью которой определяется количество затрат каждого вида, необходимое для производства одной единицы выпускаемой продукции. Поэтому в литературе часто встречаются другие формы записи:
или
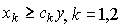
Здесь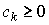 
- количество затрат вида k, необходимое для производства одной единицы продукции, а y - выпуск.
Производственная функция анализа способов производственной деятельности. Данная функция обобщает производственную функцию затрат-выпуска на случай, когда существует некоторое число (r) базовых процессов (способов производственной деятельности), каждый из которых может протекать с любой неотрицательной интенсивностью. Она имеет вид "оптимизационной задачи"
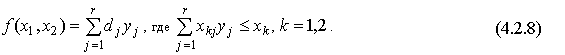
Здесь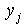 
- выпуск продукции при единичной интенсивности j -го базового процесса, 
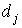- уровень интенсивности, 
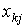- количество затрат вида k, необходимых при единичной интенсивности способа j. Как видно из (4.2.8), если выпуск, произведенный при единичной интенсивности и затраты, необходимые на единицу интенсивности, известны, то общий выпуск и общие затраты находятся путем сложения выпуска и затрат соответственно для каждого базового процесса при выбранных интенсивностях. Заметим, что задача максимизации функции f по 
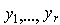в (4.2.8) при заданных ограничениях-неравенствах является моделью анализа производственной деятельности (максимизация выпуска при ограниченных ресурсах).
Линейная производственная функция (функция с взаимозамещением ресурсов) применяется при наличии линейной зависимости выпуска от затрат:
где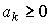 
- норма затрат k -го вида для производства единицы продукции (предельный физический продукт затрат).
