Пусть ЗЛП на максимум записана в канонической форме
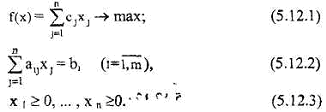
Для того чтобы записать двойственную задачу, представим ограничения – равенства (5.12.2) в виде системы равносильных неравенств
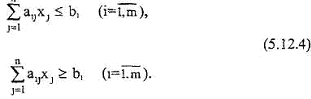
Задачу на максимум получим в виде:

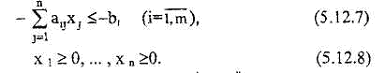
Если ввести двойственные переменные у, и у, для каждой системы ограничений (5.12.6), (5.12.7), то двойственная задача к задаче (5.12.5) – (5.12.8) будет иметь вид:
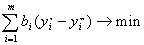 (5.12.9)
(5.12.9)
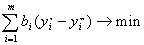 (5.12.10)
(5.12.10)
yi’≥0,yi’’≥0 i=1,...,m (5.12.11)
Теперь пусть
уi’-уi’’≡yi. (5.12.12)
Тогда переменную уi, можно считать соответствующей i-му ограничению (5.12.2) прямой задачи, а из соотношений (5.12.9) – (5.12.12) получим двойственную задачу в виде
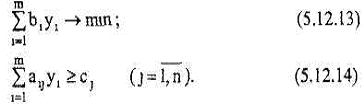
Из условий (5.12.11), (5.12 12) следует, что переменные уi могут принимать как положительные, так и отрицательные значения, а также быть равными нулю, то есть на знак этих переменных никаких ограничений не следует налагать. Задачи (5.12.1)-(5.12.3) и (5.12.13)-(5.12.14) представляют собой пару несимметричных двойственных задач:
Таблица(мах, min, несимм)
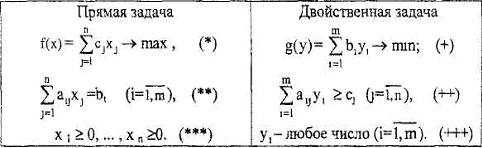
Пара несимметричных двойственных задач может быть и такой:
Таблица(min, max, несимм.)
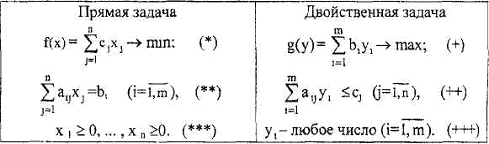
Так же формулируется двойственная задача в случае, когда в ограничения исходной задачи входят как неравенства, так и равенства.
Пусть дана пара двойственных задач.

или пара двойственных задач, записанных в таблице (min, max, несимм.).
Теорема 5.11. Для любых допустимых планов x=(x1,..,хn) и y=(y1,…, ym) прямой и двойственной ЗЛП справедливо неравенство
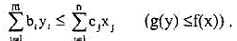 (5.12.15)
(5.12.15)
Доказательство. Учитывая неравенства (**) и (++) из таблицы (min, max) или (mm, max, несимм.) получим
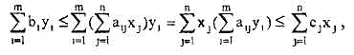
то есть получено неравенство (5.12.15).
Неравенство (5.12.15) называется основным неравенством теории двойственности.
Если прямая задача на максимум, а двойственная задача на минимум, то основное неравенство изменит только буквенные обозначения, но смысл его останется прежним: в левой части будет значение целевой функции на плане задачи на максимум, а в правой части значение целевой функции на плане задачи на минимум, как и в неравенстве (5 12 15).
При рассмотрении следующих теорем для двойственных задач будем считать, что двойственные задачи записаны в форме таблицы (min, max) или (min, max, несимм.)
Теорема 5.12 (критерий оптимальности Канторовича).
Если для некоторых допустимых планов х* и у* пары двойственных задач выполняется равенство f(x)=g(y), то х* и у* являются оптимальными планами соответствующих задач.
Доказательство. Согласно основному неравенству двойственности, для любого допустимого плана х* прямой задачи и допустимого плана у двойственной справедливо неравенство g(y) < f(x*). Но по условию g(y*) = f(x*). Отсюда в силу транзитности отношений < и =, получим g(y)< g(y*). Так как у – произвольный план, то g(y*) есть максимальное значение целевой функции, то есть у – оптимальный план двойственной задачи. Аналогично доказывается, что х* является оптимальным для прямой задачи.
Теорема 5.13 (малая теорема двойственности). Для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование допустимого плана для каждой из них.
Доказательство. Необходимость. Пусть обе задачи имеют оптимальные планы х* и у*. Это значит, что min f(x)=f(x*) и max g(y) =g(y*), то есть х* и у* принадлежат области допустимых планов.
Достаточность. Пусть каждая из пары двойственных задач имеет допустимый план. Пусть у допустимый план двойственной задачи. Тогда для любого допустимого плана у двойственной задачи, согласно основному неравенству теории двойственности (5.12.15), получим
g(y)≤f(x). (5.12.16)
Решая двойственную задачу симплексным методом, получаем последовательность опорных планов у0, у1,..., для которой последовательность g(yo), g(y1),..., g(yi), … является монотонно возрастающей (по крайней мере монотонно неубывающей). В силу неравенства (5.12.16) эта последовательность ограничена сверху. Поэтому существует допустимый план у*, для которого g(y)≤g(y*), то есть у* – оптимальный план. Аналогично доказывается существование оптимального плана х* для прямой задачи.
Теорема 5.13. Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем, экстремальные значения целевых функций равны: f(x*)=g(y*). Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива. (Доказать самостоятельно, см. например [14, стр.70]).
Теорема 5.14 (о дополняющей нежесткости). Для того чтобы планы х* и у* пары двойственных задач были оптимальными, необходимо и достаточно выполнение условий:
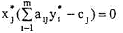 j=1,..,n (5.12.17)
j=1,..,n (5.12.17)
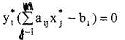 i=1,..,m (5.12.18)
i=1,..,m (5.12.18)
Доказательство. Пусть х* и у* – оптимальные планы пары двойственных задач

Согласно теореме 5.13 имеем равенство
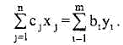
Подставив в последнее выражение Ь, из (**) для х*, получим
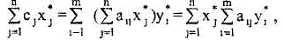
откуда
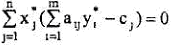
Поскольку 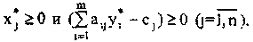 , то из (5.12.19) следует (5.12.17). Условие (5.12.18) доказывается аналогично.
, то из (5.12.19) следует (5.12.17). Условие (5.12.18) доказывается аналогично.
Пусть теперь для некоторых допустимых планов х* и у* выполняются условия (5.12.17). Просуммировав эти равенства от 1 до n, получим
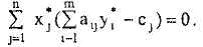
Откуда
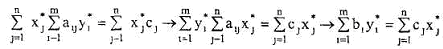
На основании критерия оптимальности Канторовича планы х* и у* оптимальны. Теорема доказана.
Следствие.
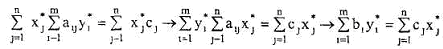
Замечание. Теорема доказана для пары двойственных задач, одна из которых записана в канонической форме. Однако, теорема остается справедливой для любой пары двойственных задач. В дальнейшем при рассмотрении метода потенциалов для транспортной задачи нам очень пригодится свойство двойственных несимметричных задач: для двойственной задачи числа у, могут быть как положительными, так и отрицательными, и нулем (i=l,m) (см. Таблицу (mах, min, несимм)).
13. Основные теоремы теории двойственности.
Теорема 1. Если одна из двойственных задач имеет конечный оптимум, то другая также имеет конечный оптимум, причем экстремальные значения целевых функций совпадают:
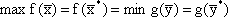 . . | (2.6) |
Если целевая функция одной из двойственных задач не ограничена, то условия другой задачи противоречивы.
Теорема 2 (о дополняющей нежесткости). Для того чтобы план 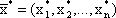 и план
и план 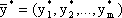 являлись оптимальными решениями, соответственно, задач (2.5) и (2.6) необходимо и достаточно, чтобы выполнялись следующие соотношения:
являлись оптимальными решениями, соответственно, задач (2.5) и (2.6) необходимо и достаточно, чтобы выполнялись следующие соотношения:
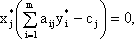 | (2.7) |
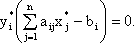 |
Таким образом, если компонент оптимального плана 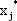 больше нуля, то при подстановке в соответствующее ограничение двойственной задачи оптимального плана
больше нуля, то при подстановке в соответствующее ограничение двойственной задачи оптимального плана 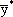 это ограничение обращается в верное равенство, и наоборот.
это ограничение обращается в верное равенство, и наоборот.
Теорема об оценках. Значения переменных 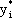 в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов bi в системе ограничений прямой задачи на величину целевой функции
в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов bi в системе ограничений прямой задачи на величину целевой функции 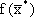 :
:
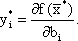 | (2.8) |
Компоненты оптимального решения двойственной задачи 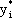 принято называть двойственными оценками. Часто употребляется также термин «объективно обусловленные оценки».
принято называть двойственными оценками. Часто употребляется также термин «объективно обусловленные оценки».
На свойствах двойственных оценок базируется экономико-математический анализ распределения ресурсов. В пределах устойчивости двойственных оценок имеют место свойства, рассмотренные ниже.
При описании свойств двойственных оценок будем пользоваться задачей о хоккейных клюшках и шахматных наборах для наглядной иллюстрации рассматриваемых положений.
Формулировка прямой (исходной) задачи:
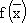 = 2x1 + 4x2 → max; = 2x1 + 4x2 → max; | |||
| |||
| x1 ≥ 0, x2 ≥ 0. |
Получим двойственную задачу.
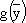 = 120y1 + 72y2 + 10y3 → min; = 120y1 + 72y2 + 10y3 → min; | |||
| |||
| y1 ≥ 0, y2 ≥ 0, y3 ≥ 0. |
В результате решения получим следующие оптимальные планы:
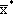 = (24, 4);
= (24, 4); 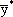 = (1/3, 1/3, 0).
= (1/3, 1/3, 0).
Легко убедиться, что при подстановке оптимальных планов в целевые функции задач оба получаемых значения равны 64.
14. Экономическая интерпретация двойственных задач.
Для проведения содержательной интерпретации двойственной задачи (II) свяжем переменные двойственной задачи
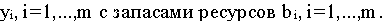
Пусть L* - максимальное значение дохода в задаче (I). Если запасы ресурсов 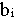 , i=1,...,m изменить, то может измениться и максимальный доход L*. Это означает, что L* является функцией от ресурсов
, i=1,...,m изменить, то может измениться и максимальный доход L*. Это означает, что L* является функцией от ресурсов 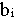 , i=1,...,m, т.е.
, i=1,...,m, т.е.
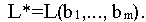
Рассмотрим отношение приращения дохода 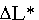 к приращению i-го ресурса
к приращению i-го ресурса 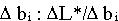 ;
;
Тогда по определению частной производной функции
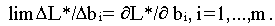
Но по первой теореме двойственности оптимальное значение целевой функции прямой задачи совпадает с оптимальным значением целевой функции двойственной задачи
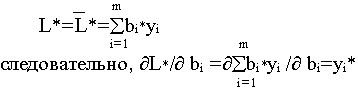
Таким образом, оптимальное значение двойственной переменной 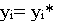
числено равно дополнительному доходу 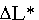 при увеличении i-го ресурса на единицу, если величина
при увеличении i-го ресурса на единицу, если величина 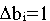 является достаточно малой по сравнению с величиной
является достаточно малой по сравнению с величиной 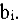 Полученный вывод имеет очень важное практическое применение. Пусть L*- максимальное значение дохода в задаче (I),
Полученный вывод имеет очень важное практическое применение. Пусть L*- максимальное значение дохода в задаче (I),
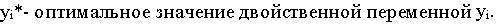
Тогда, изменяя i-й ресурс на единицу, получим новое значение максимального дохода по формуле
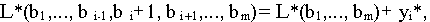
или более общий вид
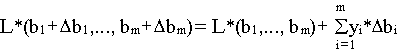
Двойственные переменные
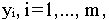
называются оценками (теневыми ценами, ценностями) соответствующих ресурсов i=1,..., m, и характеризуют меру эффективности использования соответствующих ресурсов.
15. Линейная модель баланса межотраслевых материально-вещественных связей.
Выводы:
1. Межотраслевой баланс – это таблица, характеризующая
связи между экономическими объектами, входящими в экономическую систему.
2. Различают межотраслевой баланс в натуральном и стоимостном выражении.
3. Межотраслевой баланс состоит из четырех квадрантов. I квадрант – его важнейшая часть. В нем содержится информация о межотраслевых связях.
4. Вся произведенная внутри экономической системы продукция потребляется. Часть ее в форме суммарного производственного потребления идет на производственные нужды отраслей, входящих в экономическую систему. Другая часть потребляется в форме конечного продукта.
5. I и II квадранты отражают баланс между производством и
потреблением.
6. I и III квадранты отражают стоимостную структуру продукции каждой отрасли.
7. Суммарный конечный продукт равен суммарной условно чистой продукции.
8. Межотраслевой баланс был построен по данным отчетного
периода (например, истекшего года),
9. С построением балансовой таблицы завершается первый этап решения задачи методом математического моделирования: выявлены объекты изучения, установлены существенные связи между ними, собрана статистическая информация.
 2015-09-06
2015-09-06 1000
1000