2014-02-09
3413
Рисунок 1.5.2. Кривая спроса при доходе, превышающем Сtr и участок Гиффена
Литература
1. Леонтович А. В. Элементарное пособие к применению методов Gauss'a и Pearson'a при оценке ошибок в статистике и биологии. Киев, 1911.
2. Слуцкий Е. Е. Теория корреляции и элементы учения о кривых распределения // Изв. Киев. коммерч. ин-та. 1912. Кн. XVI. С. IV+208. (Слуцкий Е. Е. Теория корреляции... Киев, 1912).
3. Чупров А.А. [Рец. на кн.: Слуцкий Е. Е. Теория корреляции и элементы учения о кривых распределения. Киев, 1912].
4. Слуцкий Е.Е. Сэр Вильям Петти: Краткий очерк его экономических воззрений с приложением нескольких важнейших отрывков из его произведений // Студ. бюл. Киев. коммерч. ин-та. 1914. ╧ 16-18. С. 5-48. (Слуцкий Е.Е. Сэр Вильям Петти... Киев, 1914. 48 с.).
5. Там же. С. 25.
6. Там же. С. 24.
7. Кейнс Дж. М. Общая теория занятости, процента и дене г. М., 1978; Лист Ф. Национальная система политической экономии. М., 1891.
8. Слуцкий Е.Е. Сэр Вильям Петти... С. 22.
9. Slutsky Е. Е. On the criterion of goodness of fit of the regression lines and the best method of fittingthem to the data // J. Royal Statist. Soc. 1914. Vol. 77, pt. I (Dec. 1913). P. 78-84.
10. Фишер Р. Статистические методы для исследователей: Пер. с англ. М., 1958.
11. Слуцкий Е. Е. 1) Статистика и математика. [Рец. на кн.: Кауфман А. А. Теория и методы статистики] // Стат. вестн. 1915-1916. Кн. 3-4. С. 1-17; 2) Об одной ошибке в применении формулы теории корреляции // Там же. С. 18-19.
12. Slutsky Е.Е. Sulla teoria sel bilancio del consumatore // G. Econ. Riv. Statist. 1915. Vol. 51, N 1. P. 1-26.
13. Цит. по: Слуцкий Е.Е. К теории сбалансированного бюджета потребителя//Экономико-математические методы. М., 1963. С. 241.
14. Там же. С. 243-245.
15. Там же. С.248.
16. Там же. С. 260-261.
17. Там же. С. 256.
18. Там же. С. 258.
19. Там же. С. 267.
20. Цит. по: Четвериков Н. С. Жизнь и научная деятельность Е. Е. Слуцкого (1880- 1948) // Учен. зап. по статистике / АН СССР. М., 1959. Т. 5. С. 256.
21. Слуцкий Е.Е. К вопросу о вычислении дохода государства от эмиссии // Местное хоз-во. Киев, 1923. ╧ 2, нояб. (Приложение I к ст.: Яснопольский Н. П. Наше денежное обращение в эпоху революции).
22. Там же. С. 49.
23. Slutzhl E.E. Ein Beitrag zur Formal-praxeologischen Grundlegung der Oekonomik / Akad. Oukrainienne des Sciences // Ann. de la classe des sci. soc,-econ. Kiev, 1926. Vol. 4. P. 3-12. - Пер. с нем.: Этюд до проблемы будування формально-праксеолопчных засад эконом1ки / Пер. с нем. Б. А. Язловского // Зап. соц.-экон. в1дд1лу Укр. Акад. наук. Ki'ев, 1926. Т. 4. С. 1-11.
24. Slutzhi Е. Е. Zur Kritik des Bohm-Bawerkschen Wertbegriffs und seiner Lehre von der Messbarkeit des Wertes // Schmollers Jb. 1927. Bd. 51. H. 4. S. 37-52.
25. Слуцкий E.E. О новом коэффициенте средней плотности населения // Вестн. статистики. М., 1923. Т. 13.
26. Слуцкий Е. Е. К вопросу о логических основах исчисления вероятностей // Там же. 1922. ╧ 12. С. 12-21.
27. Слуцкий Е. Е. Сложение случайных причин как источник циклических процессов // Вопр. конъюнктуры. М., 1927. Т. 3, вып. I. С. 34-64. - Англ. пер.:
The summation of random causes as the sources of cyclik processes // Ibid. C. 156-160.
28. Yule G. On a method of investigating periodicities in disturbed series, with special reference to Wolfer's sunspot numbers. Phil., 1927.
29. Slutsky E. Ueber stochastische Asymptoten und Grenzwerte // Metron (Padova). 1925. Vol. 5, N 3. P. 3-89.
30. Слуцкий Е. Е. Жизнеописание. 3 декабря 1942 г. (Рукопись).
31. Таблицы для расчетов неполной гамма-функции и распределения хи-квадрат / Сост. Е. Е. Слуцкий. М., 1950.
32. Колмогоров А.Н. Некролог // Усп. мат. наук. 1948. Т. 3, вып. 4.
1Письмо Е. Е. Слуцкого - Ю. Н. Володкевич от 4 апреля 1903 г.
2За книгу стихов "Жертвенные песни" (Гитанджали), переведенную на английский язык самим автором и изданную в 1912 г., Тагору была присуждена Нобелевская премия по литературе за 1913 г.
3Перевод Е. Е. Слуцкого публикуется впервые. Обнаружен в 1998 г. А. Г. Волковым в личном архиве Н. А. Свавицкого.
НЕСКОЛЬКО СЛОВ О "ПАРАДОКСЕ" ГИФФЕНА
Полученные в предыдущем параграфе кривые спроса противоречат канонам классической теоретической экономики. Кто-то из читателей готов заявить, что новые типы кривых спроса вообще противоречат смыслу. На самом деле это не так. Полученные мною построения вовсе не являются чем-то удивительным, парадоксальным и выходящим из ряда вон. Как раз именно они позволяют свести известные в экономике явления, которые до сих пор представлялись некоторым парадоксом, в единую и целостную систему, не оставляя в ней никаких исключений.
Самым лучшим доказательством этому утверждению будут служить явления, кажущиеся парадоксальными с позиций классической теории, рассматривающей рыночное равновесие на плоскости.
Самый известный парадокс в экономической теории - "парадокс Гиффена". Английский экономист прошлого века Р.Гиффен обратил внимание на то, что во время голода в Ирландии в середине XIX века объем спроса на картофель существенно увеличился при росте цен на него, что полностью противоречит классической постановке закона спроса - при росте цены на товар объем приобретаемого товара должен уменьшаться.
Это явление и получило название "парадокса Гиффена". В экономической теории, которая рассматривает множество различных товаров, даже выделяют особо нормальные товары и "товары Гиффена"
Парадокс Гиффена экономистами объясняется следующим образом: "Дело в том, что картофель представлял основной продукт питания ирландских бедняков. Повышение его цены вынудило их сократить потребление других, более дорогих и качественных продуктов. Поскольку все же картофель оставался сравнительно наиболее дешевым продуктом, объем спроса на него вырос... подобная ситуация представляет единственно возможное исключение из общего закона спроса".
Впрочем, в других отечественных научных источниках я встречал ту же самую историю, только не с картофелем, а с хлебом. И не с ирландскими бедняками, а с английскими. Но это не меняет сути изученного явления.
Таким образом "парадокс Гиффена" рассматривается как исключение из закона. Есть несколько очень логичных интерпретаций этого явления в более сложной постановке, в том числе и с помощью инструментария математического моделирования, когда рассматривается общая система взаимосвязей товаров, цен, объемов и доходов. При этом приходится делать ряд допущений о замкнутости системы, о характере доходов и т.п.
К тому же известно, что открытое Гиффеном явление вовсе не является исключением из совокупности всех экономических наблюдений, именно поэтому теоретики и говорят о "товарах Гиффена", а не об одном товаре.
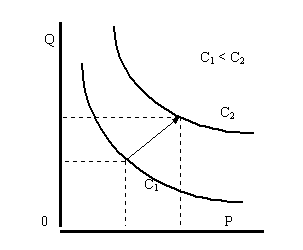
Рисунок 1.5.1. Классические кривые спроса и "парадокс Гиффена"
Если рассматривать кривую спроса в классической постановке (рисунок1.5.1), то легко убедиться в том, что действительно по закону спроса такое поведение потребителей в принципе невозможно - с увеличением цен на товар объемы его приобретения должны уменьшаться, но не увеличиваться. Увеличение объемов спроса при одновременном увеличении цен по сути классической теории означает переход от старой кривой спроса при доходе C1 к новой кривой спроса при новых, более высоких доходах C2, что показано стрелкой на рисунке 1.5.1.
Рассмотрю данный парадокс в полученной выше интерпретации. Для этого воспользуюсь графиком рисунка 1.4.5 и изображу его на новом рисунке 1.5.2.
Так как картофель составлял основной продукт питания, то вполне логично предположить, что товар находился на том участке поведения поверхности спроса, который характерен для дохода, превышающего Сtr, то есть объем потребления миновал стадию "ажиотажного потребления".
Так как картофель к тому же является одним из самых дешевых продуктов питания и его цена невелика, вполне очевидно, что участок кривой спроса, соответствующий этому состоянию рынка, находится в первой части графика рисунка 1.5.2.
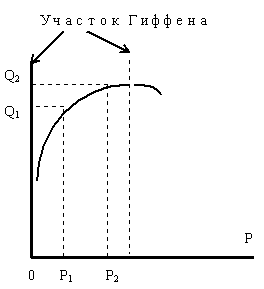
Если при этом в некоторый момент времени продавцы назначают цену товара, равную Р1, то объемы потребления будут равны Q1. Уменьшение цены на картофель, как это не парадоксально звучит, но вполне логично следует из рисунка 1.5.2, приведет к снижению объемов закупок, а ее повышение приведет к увеличению закупок. В случае, изученном Р.Гиффеном, произошло последнее - цены на картофель были повышены до размеров Р2, а объемы продаж картофеля увеличились до Q2. Как следует из графика рисунка 1.5.2, дальнейшее увеличение цен в конечном итоге привело бы к падению объемов приобретения картофеля.
Таким образом, следует признать, что "парадокс Гиффена" вовсе не является парадоксом, нарушающим экономические законы и служащим исключением из правил, а является вполне естественным элементом общей системы рыночного равновесия, если рассматривать это равновесие в пространстве "цена-объем-доход".
Аналогичное поведение некоторых товаров можно обнаружить и в современном мире в экономической жизни любой страны, так как обязательно существует такой товар, потребление которого при данных доходах потребителей соответствует характеру рисунка 1.5.2. При этом вовсе не обязательно, что таким товаром должен быть дешевый продукт типа картофеля. В экономически развитых странах такими товарами могут быть и предметы роскоши. Действительно, выше было показано (рисунок 1.4.9), что кривая спроса, полученная для товара, не являющегося товаром повседневного спроса, может иметь в отдельных случаях точно такую же форму, как только что рассмотренная кривая, и на ней также должен быть участок Гиффена.
Еще в начале XX века дискутировался вопрос о возможном существовании графиков спроса, имеющих положительный угол наклона касательной к графику. В результате этой и других дискуссий было единодушно решено, что подобное поведение кривых спроса считалось и считается своеобразным исключением из правила. А из всего сказанного в данном параграфе, следует как раз вывод о том, что выявленное впервые Гиффеном поведение потребителя не является "парадоксом" в рыночной экономике, а является вполне реальной закономерностью, дополняющей классическое поведение спроса, и поэтому его не следует называть "парадоксом". Эффект Веблена, который зачастую приводят в книгах по экономической теории как некоторое взаимосвязанное с парадоксом Гиффена явление, подтверждает это утверждение.
Здесь уместно сделать еще одно важное замечание. В самом начале книги я предложил по-другому изобразить графическую модель кривых спроса и предложения и расположить оси координат в соответствии с их математическим смыслом. Если бы этого не было сделано, было бы очень сложно построить поверхность спроса, и уж совсем проблематично было бы построение тех кривых спроса, которые получены в данном параграфе.
Зависимости в уравнении производственной функции от затрат труда и капитала окажут помощь начинающему трейдеру в достижении результатов на рынке форекс.
Идея производственной функции была впервые предложена американским экономистом П. Дугласом и математиком Ч. Коббом в 1928 г. в виде функции в которой фигурируют только два фактора: затраты труда и капитала. Эта упрощенная форма (в которой не учитываются затраты природных ресурсов) получила большое распространение в силу трудностей учета затрат природных ресурсов, и лишь в последние годы начали предприниматься попытки учесть вклад всех трех факторов.
В 30-е гг. голландский экономист Ян Тинберген (ставший впоследствии Нобелевским лауреатом) показал, что параметр, характеризующий технологию производства, меняется во времени.
Согласно оценкам Тинбергена, сделанным им для нескольких стран на период 1870—1914 гг., в Германии экстенсивные факторы обеспечили 60% роста, интенсивные (технический прогресс) — 40; в Великобритании — соответственно 80 и 20, в США —73 и 27%.
https://slovari.yandex.ru/dict/lopatnikov/article/lop/lop-0580.htm
| Экономико-математический словарь КОББА-ДУГЛАСА ФУНКЦИЯ [Cobb-Douglas production function] - производственная функция, примененная американскими исследователями Ч. Коббом и П. Дугласом при анализе развития экономики США в 20-30-х гг. ХХ века. Имеет простую алгебраическую форму: N = A · L α K β, где N - национальный доход; A - коэффициент размерности; L и K - соответственно объемы приложенного труда и капитала; α и β - константы (коэффициенты эластичности производства по труду L и капиталу K). Функция - однородная степени α+β; следовательно, увеличение L и K в одинаковое число раз m увеличивает доход в m α+β раз. Если сумма α+β равна единице - функция линейно однородная; если больше или меньше единицы, имеет место эффект масштаба (соответственно положительный или отрицательный). К.-Д. ф. основывается на предположениях о понижающейся предельной отдаче ресурсов (см. Закон убывающей отдачи, Предельный эффект затрат), постоянстве коэффициентов эластичности производства по затратам ресурсов. Эластичность замещения ресурсов в любой точке кривой К.-Д. ф. равна единице. Хотя К.-Д. ф. нельзя отнести к линейным, значения параметров А, α, β можно оценить с помощью линейного регрессионного анализа по методу наименьших квадратов. Для этого ее приводят к линейному виду, прологарифмировав обе части уравнения (обычно здесь берутся натуральные логарифмы): lnN = ln А + α lnL + β lnK. Модификация функции, учитывающая технический прогресс, достигается введением дополнительного сомножителя e π, где π - темп технического прогресса (константа). |
https://www.sseu.ru/edumat/v_mat/gloss/g330.htm
Типичным примером производственной функции степенного вида является функция Кобба - Дугласа. В 1928 г. Ч. Кобб и
П. Дуглас на основе данных по обрабатывающей промышленности США за период 1899 - 1922 гг. представили функцию
Р = b L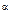 
K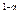
,
где Р - расчетный индекс производства; К - индекс основного капитала; L - индекс занятости. Это была первая эмпирическая производственная функция, построенная по данным временных рядов.
Определение. Производственная функция Кобба - Дугласа устанавливает зависимость величины созданного общественного продукта от совокупных затрат живого труда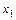 
и суммарного объема применяемых производственных фондов 
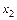. Она имеет следующий вид:
,
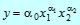где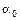 
- коэффициент, учитывающий влияние факторов, не вошедших в это уравнение, их конкретные числовые значения определяются на основе статистических данных с помощью корреляционных методов, соблюдаются условия 
.
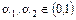Хотя каждый из коэффициентов меньше 1, их сумма может быть меньше, равна или больше 1. Эта сумма показывает эффект одновременного пропорционального увеличения объема как ресурсов труда, так и производственных фондов.
https://nit.miem.edu.ru/cgi-bin/article?id=122
