Матрицы прямых и полных материальных затрат

. Статистические межотраслевые модели используются для разработки планов выпуска и потребления продукции и основываются на соотношениях межотраслевого баланса.

При построении модели делают следующие предположения:

1) все продукты, производимые одной отраслью, однородны и рассматриваются как единое целое, т.е. фактически предполагается, что каждая отрасль производит один продукт;

2) в каждой отрасли имеется единственная технология производства;

3) нормы производственных затрат не зависят от объёма выпускаемой продукции;

4) не допускается замещение одного сырья другим.

В действительности эти предположения, конечно, не выполняются. Даже на отдельном предприятии обычно выпускаются различные виды продукции, используются различные технологии, удельные затраты зависят от объема выпуска и в тех или иных пределах допускается замена одного сырья другим. Следовательно, эти предположения тем более неверны для отрасли. Однако такие модели получили широкое распространение и, как показала практика, они вполне адекватны и применимы для составления планов выпуска продукции.

При этих предположениях величина x_ij может быть представлена следующим образом:

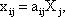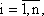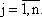(3.3)

Величина a_ij называется коэффициентом прямых материальных затрат. Она показывает, какое количество продукции i-й отрасли идет на производство единицы продукции j-й отрасли. Коэффициенты a_ij считаются в межотраслевой модели постоянными.

Подставляя выражение (3.3) в формулу (3.1), получим:

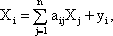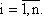Это соотношение можно записать в матричном виде:

X = AX + Y,

(3.4)

где X = (X₁, X₂,..., X_n) - вектор валовых выпуков;

Y = (y₁, y₂,..., y_n) - вектор конечного продукта;

A = 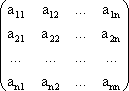- матрица коэффициентов прямых материальных затрат.

Коэффициенты прямых материальных затрат являются основными параметрами статической межотрслевой модели. Их значения могут быть получены двумя путями:

1) статистически. Коэффициенты определяются на основе анализа отчётных балансов за прошлые годы. Их неизменность во времени определяется подходящим выбором отраслей;

2) нормативно. Предполагается, что отрасль состоит из отдельных производств, для которых уже разработаны нормативы затрат; на их основе рассчитываются среднеотраслевые коэффициенты.

Выражение (3.4) принято называть балансом распределения продукции. Его можно использовать для анализа и планирования структуры экономики. Если известны коэффициенты прямых материальных затрат, то, задав конечный продукт по каждой отрасли, можно определить необходимые валовые выпуски отраслей. В этом заложена основная идея использования матричных моделей для планирования производства.

Преобразуем выражение (3.4):

X - AX = Y,
X (E - A) = Y,
X = (E - A)^-1Y,	(3.5)

где E - единичная матрица.

До начала планирования следует выяснить, существует ли матрица, обратная матрице (E-A), и не будут ли получены отрицательные значения выпуска по отраслям.

Установим некоторые свойства коэффициентов прямых материальных затрат.

1. Неотрицательность, т.е. a_ij ≥ 0, 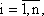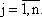Это утверждение следует из неотрицательности величин x_ij и положительности валовых выпусков X_j.

2. Сумма элементов матрицы A по любому из столбцов меньше единицы, т.е.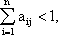

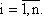
Доказать это утверждение несложно.

Для любой отрасли условно чистая продукция есть величина положительная, поскольку включает в себя заработную плату, амортизацию, прибыль и т.д., т.е. V_j>0. Поэтому, используя соотношение (3.2), можно записать:

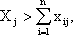из соотношения (3.3):

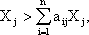откуда безусловно следует:

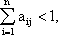таким образом, утверждение доказано.

Можно показать, что при выполнении этих двух условий матрица B = (E - A)^-1 существует и если ее элементы неотрицательны. Говорят, что в этом случае матрица прямых затрат А является продуктивной.

Перепишем формулу (3.5):

X = BY,

(3.6)

Матрица В носит название матрицы полных материальных затрат, а ее элементы b_ij называют коэффициентами полных материальных затрат. Коэффициент b_ij показывает, каков должен быть валовый выпуск i-й отрасли для того, чтобы обеспечить выпуск единицы конечного продукта j-й отрасли.

Можно показать, что

B = E + A + A² + A³ +...

(3.7)

Умножим обе части на (E - A):

B(E - A) = (E + A + A² + A³ +...)(E - A),
B(E - A) = E + A + A² + A³ +..- A - A² - A³ -...,
B(E - A) = E,
B = E / (E - A),
B = (E - A)^-1.

Доказано.

Из сотношения (3.7) следует b_ij ≥ a_ij, 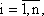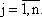Таким образом, коэффициент полных материальных затрат b_ij, описывающий потребность в выпуске продукции i-й отрасли в расчете на единицу конечного продукта j-й отрасли, не меньше коэффициента прямых материальных затрат a_ij, рассчтываемого на единицу валового выпуска.

Кроме того, из соотношения (3.7) для диагональных элементов матрицы B следует:

b_ii ≥ 1,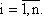

16. Производственные функции выпуска продукции. Средние и предельные характеристики, нормы замещения ресурсов. Основные виды производственных функций. Функция Коб ба-Дугласа.

В реальной жизни в пределах используемой технологии предприниматель стремится найти наилучшее сочетание факторов производства, с тем чтобы достичь наибольшего выхода продукции. Отношение между любым набором факторов производства и максимально возможным объемом продукции, производимой из этого набора факторов, характеризует производственную функцию.

Производственная функция — технологическая зависимость между затратами ресурсов и выпуском продукции.

В микроэкономике используется большое количество самых разнообразных функций производства, но чаще всего — двухфакторные функции вида: 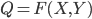, которые легче анализировать в силу их графического представления.

Среди двухфакторынх функций наибольшую известность получила функция Кобба-Дугласа, имеющая вид:

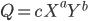
где:

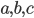§ — положительные константы

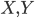§ — количество используемых ресурсов (обычно рассматривают труд и капитал)

Производственная функция характеризует техническую зависимость между ресурсами и выпуском и описывает всю совокупность технологически эффективных способов. Каждый способ может быть описан своей производственной функцией.

1 2 3 4 5 6

Подборка статей по вашей теме: