Лабораторная работа № 1
ИЗМЕРЕНИЕ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ
ВОЗДУХА МЕТОДОМ НАГРЕТОЙ НИТИ
Цель работы: экспериментальное определение температурной зависимости коэффициента теплопроводности воздуха.
Оборудование: экспериментальная установка ФПТ1-3
Краткая теория и методика выполнения работы
Явление теплопроводности представляет собой процесс переноса тепла, обусловленный беспорядочным движением молекул. Для переноса тепла в любом веществе необходимо и достаточно существования в нем областей с разными температурами, т.е. наличие неоднородностей в температурном поле. В этом случае температура будет являться функцией пространственных координат. Мерой неоднородностей в температурном поле служит градиент температуры 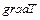 . Он определяется как вектор, направленный в данной точке по нормали к изотермической поверхности (поверхности одинаковой температуры) в сторону возрастания температуры. Для малых изменений температуры вдоль одной из координатных осей (рассмотрим одномерный случай), величина
. Он определяется как вектор, направленный в данной точке по нормали к изотермической поверхности (поверхности одинаковой температуры) в сторону возрастания температуры. Для малых изменений температуры вдоль одной из координатных осей (рассмотрим одномерный случай), величина 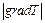 равна
равна 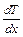 и характеризует изменение температуры на единицу длины по направлению нормали
и характеризует изменение температуры на единицу длины по направлению нормали 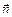 к изотермической поверхности в данной точке:
к изотермической поверхности в данной точке:
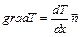 . (1.1)
. (1.1)
Для количественной характеристики переноса тепла теплопроводностью вводится понятие вектора плотности потока тепла 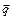 . Он направлен по нормали к изотермической поверхности в данной точке, а его величина равна количеству тепла, переносимому через единицу площади изотермической поверхности (в окрестности данной точки) в единицу времени.
. Он направлен по нормали к изотермической поверхности в данной точке, а его величина равна количеству тепла, переносимому через единицу площади изотермической поверхности (в окрестности данной точки) в единицу времени.
Полученный опытным путем закон Фурье утверждает, что вектор плотности потока тепла пропорционален градиенту температуры:
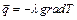 . (1.2)
. (1.2)
Коэффициент пропорциональности 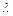 называется коэффициентом теплопроводности вещества. Знак минус учитывает тот факт, что поток тепла направлен в сторону противоположную направлению градиента температуры, т.е. тепло переносится в сторону уменьшения температуры. Для одномерного случая, с учетом определения градиента (1.1), закон Фурье (1.2) принимает вид:
называется коэффициентом теплопроводности вещества. Знак минус учитывает тот факт, что поток тепла направлен в сторону противоположную направлению градиента температуры, т.е. тепло переносится в сторону уменьшения температуры. Для одномерного случая, с учетом определения градиента (1.1), закон Фурье (1.2) принимает вид:
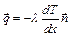 . (1.3)
. (1.3)
Одним из наиболее распространенных методов измерения коэффициента теплопроводности газов является метод нагретой нити. Исследуемый газ находится в цилиндрической трубке, по оси которой натянута нить из вольфрама, служащая источником тепла. На всей наружной поверхности трубки поддерживается одинаковая и постоянная температура, а через нить пропускается электрический ток. В случае длинных трубки и нити (их длина должна быть много больше радиуса трубки) из соображений симметрии следует, что изотермическими поверхностями в газе будут цилиндрические поверхности с общей осью - осью нити. Направление нормали к этим поверхностям есть, очевидно, радиальное направление.
Через любую такую цилиндрическую поверхность за время 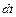 пройдет количество тепла, равное:
пройдет количество тепла, равное:
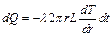 , (1.4)
, (1.4)
где 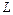 – длина цилиндрической трубки,
– длина цилиндрической трубки, 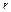 – ее радиус.
– ее радиус.
Мощность теплового потока 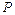 определяется как:
определяется как:
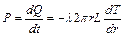 . (1.5)
. (1.5)
Полученное дифференциальное уравнение решается методом разделения переменных. Получим:
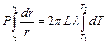 , (1.6)
, (1.6)
где 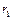 – внутренний радиус трубки,
– внутренний радиус трубки, 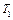 – температура газа у внутренней поверхности трубки;
– температура газа у внутренней поверхности трубки; 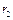 – радиус вольфрамовой нити,
– радиус вольфрамовой нити, 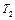 – ее температура.
– ее температура.
Тогда для коэффициента теплопроводности имеем следующее выражение:
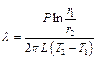 . (1.7)
. (1.7)
Для стационарного процесса 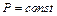 . В установившемся режиме, т.е. когда газ в каждой точке пространства внутри трубки уже прогрелся до постоянной температуры
. В установившемся режиме, т.е. когда газ в каждой точке пространства внутри трубки уже прогрелся до постоянной температуры 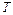 , можно принять, что все тепло, выделяющееся в проволоке, при прохождении по ней электрического тока, переносится за счет теплопроводности газа к стенке трубки. Постоянная тепловая мощность, выделяемая на нити:
, можно принять, что все тепло, выделяющееся в проволоке, при прохождении по ней электрического тока, переносится за счет теплопроводности газа к стенке трубки. Постоянная тепловая мощность, выделяемая на нити:
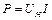 , (1.8)
, (1.8)
где 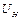 и
и 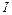 – падение напряжения на вольфрамовой нити и ток, протекающий по ней.
– падение напряжения на вольфрамовой нити и ток, протекающий по ней.
Таким образом, чтобы определить коэффициент теплопроводности, надо знать:
а) количество тепла, переносимое от проволоки к стенке трубки в единицу времени 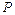 ;
;
б) разность температур между слоями газа, непосредственно прилегающими к поверхностям нити и трубки;
в) размеры нити и трубки.
За температуру стенки трубки 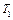 принимают температуру воздуха в лаборатории, в котором трубка находится и которая измеряется термометром. Температуру проволоки
принимают температуру воздуха в лаборатории, в котором трубка находится и которая измеряется термометром. Температуру проволоки 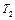 можно определить, измерив изменение электрического сопротивления при её нагревании. Действительно, в области используемых температур сопротивление нити растет с температурой по линейному закону, т.е.
можно определить, измерив изменение электрического сопротивления при её нагревании. Действительно, в области используемых температур сопротивление нити растет с температурой по линейному закону, т.е.
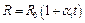 , (1.9)
, (1.9)
где 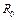 – сопротивление нити при
– сопротивление нити при 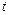 = 0 ° С,
= 0 ° С, 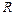 – ее сопротивление при температуре
– ее сопротивление при температуре 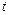 ,
, 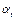 – температурный коэффициент сопротивления в ° С -1,
– температурный коэффициент сопротивления в ° С -1, 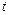 – температура в ° С.
– температура в ° С.
Измерив сопротивление нити 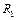 до ее нагревания, т.е. при
до ее нагревания, т.е. при 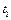 , а затем сопротивление
, а затем сопротивление 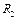 после ее нагревании до температуры
после ее нагревании до температуры 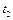 получим:
получим:
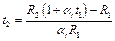 . (1.10)
. (1.10)
Таким образом, определяя на основании (1.10) температуру нагретой нити и подставляя ее значения в (1.7), можем вычислить значение 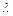 , соответствующее этой температуре.
, соответствующее этой температуре.
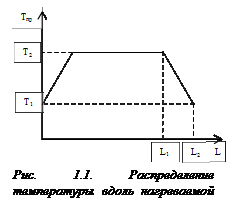
Рассмотрим некоторые источники систематических погрешностей, которые возникают при проведении эксперимента. Во-первых, концы нити поддерживаются при температуре, близкой к комнатной 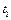 . Поэтому, вследствие теплопроводности металла, по всей длине нити устанавливается распределение температур, показанное на рис. 1.1.
. Поэтому, вследствие теплопроводности металла, по всей длине нити устанавливается распределение температур, показанное на рис. 1.1.
 Утечку тепла через концы нити можно учесть опытным путем, используя не одну нить, а две одинакового материала и различной длины. В настоящей работе будем считать, что температура постоянна по всей длине нити.
Утечку тепла через концы нити можно учесть опытным путем, используя не одну нить, а две одинакового материала и различной длины. В настоящей работе будем считать, что температура постоянна по всей длине нити.
Во-вторых, тепловое излучение поверхности нагретой нити является дополнительным, наряду с теплопроводностью, механизмом переноса тепла от нити в окружающую среду. Для оценки количества тепла, отдаваемого нитью за счет излучения, можно воспользоваться законом Стефана-Больцмана, по которому с единицы поверхности абсолютно черного тела за единицу времени излучается энергия:
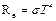 , (1.11)
, (1.11)
где 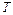 – абсолютная температура черного тела в К, а
– абсолютная температура черного тела в К, а 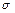 = 5,67×10-8 Вт /(м 2 К 4). Любое тело, которое не является абсолютно черным, при той же температуре излучает меньшую энергию:
= 5,67×10-8 Вт /(м 2 К 4). Любое тело, которое не является абсолютно черным, при той же температуре излучает меньшую энергию:
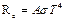 , (1.12)
, (1.12)
где 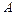 – поглощательная способность тела. Для всех тел
– поглощательная способность тела. Для всех тел 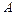 <1 (для вольфрама
<1 (для вольфрама 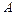 = 0,4). Если
= 0,4). Если 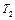 – абсолютная температура нагретой нити,
– абсолютная температура нагретой нити, 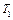 – температура стенки трубки и если считать, что все излучение нити попадает на стенку трубки, то энергия, отдаваемая в единицу времени через излучение, будет определяться соотношением:
– температура стенки трубки и если считать, что все излучение нити попадает на стенку трубки, то энергия, отдаваемая в единицу времени через излучение, будет определяться соотношением:
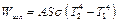 , (1.13)
, (1.13)
где 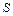 – площадь поверхности нити.
– площадь поверхности нити.
 2015-09-06
2015-09-06 1089
1089







