Понятие внутренней энергии тела включает в себя кинетическую энергию движения молекул, кинетическую энергию движения атомов внутри молекул, кинетическую энергию частиц, входящих в состав атомов, потенциальную энергию взаимодействия молекул между собой и атомов внутри молекул. Для идеального газа отсутствует взаимодействие молекул между собой, и его внутренняя энергия будет полностью определяться кинетической энергией всех видов движения, в которых может участвовать молекула.
Средняя кинетическая энергия одноатомной молекулы идеального газа определяется выражением:
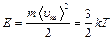 , (2.1)
, (2.1)
где 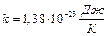 – постоянная Больцмана,
– постоянная Больцмана, 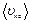 – средняя квадратичная скорость молекулы,
– средняя квадратичная скорость молекулы, 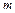 – масса молекулы,
– масса молекулы, 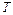 – температура газа.
– температура газа.
По теореме Больцмана при тепловом равновесии для данной температуры 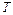 средняя кинетическая энергия молекулы равномерно распределена между степенями свободы молекулы и для каждой степени свободы равна
средняя кинетическая энергия молекулы равномерно распределена между степенями свободы молекулы и для каждой степени свободы равна 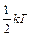 .
.
Под числом степеней свободы тела подразумевается число независимых координат, которое нужно ввести для полного определения положения тела в пространстве. Положение одноатомной молекулы в декартовой системе координат при ее поступательном движении определяется тремя координатами, т.е. молекула имеет три поступательные степени свободы.
Двухатомную молекулу обычно представляют в форме гантели (жесткая связь), центр которой совпадает с началом координат. Такая молекула может двигаться поступательно как целое в трех взаимно перпендикулярных направлениях. Кроме того, молекула может вращаться вокруг этих же осей, причем вращение вокруг оси, проходящей по линии соединяющей атомы, не изменяет положения системы в пространстве и лишено смысла. Таким образом, для определения положения двухатомной молекулы в пространстве необходимо задать пять степеней свободы (три поступательные и две вращательные). Трехатомная нелинейная молекула имеет шесть степеней свободы – три поступательных и три вращательных.
При температурах выше 1000  в молекуле имеет место интенсивное колебательное движение атомов. Поэтому при распределении энергии необходимо учитывать и колебательные степени свободы.
в молекуле имеет место интенсивное колебательное движение атомов. Поэтому при распределении энергии необходимо учитывать и колебательные степени свободы.
Было установлено, что двухатомная молекула имеет одну колебательную степень свободы, трехатомная нелинейная – три, четырехатомная – шесть.
Общее число степеней свободы (поступательные iпоступ, вращательные iвр и колебательные iкол) в 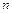 – атомной молекуле равно
– атомной молекуле равно 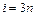 , из них
, из них 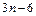 – колебательные степени свободы.
– колебательные степени свободы.
Закон распределения энергииимеет место и для вращательных, и для колебательных степеней свободы. На каждую вращательную степень свободы также приходится энергия 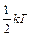 . Если амплитуда колебаний мала по сравнению с расстояниями между атомами, то колебания можно считать гармоническими. На каждую колебательную степень свободы приходится энергия, равная
. Если амплитуда колебаний мала по сравнению с расстояниями между атомами, то колебания можно считать гармоническими. На каждую колебательную степень свободы приходится энергия, равная 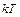 (
(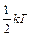 в виде кинетической и
в виде кинетической и 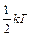 –потенциальной энергии).
–потенциальной энергии).
Следовательно, среднее значение энергии молекулы равно:
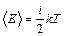 ,
,
где 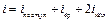 .
.
Внутренняя энергия одного моля газа находится как:
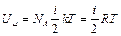 ,
,
где 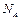 – число Авогадро,
– число Авогадро, 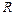 – универсальная газовая постоянная
– универсальная газовая постоянная 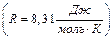 . Таким образом, внутренняя энергия определяется числом степеней свободы и температурой газа:
. Таким образом, внутренняя энергия определяется числом степеней свободы и температурой газа:
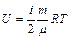 .
.
Изменение внутренней энергии системы может быть осуществлено двумя путями:
1) путем передачи системе (или от системы) некоторого количества теплоты 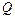 ;
;
2) путем совершения системой работы против внешних сил (или совершения внешними силами работы над системой).
Закон сохранения энергии в этом случае формулируется следующим образом: переданное системе количество теплоты идет на изменение внутренней энергии системы и на совершаемую системой работу (I закон термодинамики или первое начало термодинамики):
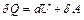 . (2.2)
. (2.2)
В (2.2) 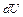 представляет собой полный дифференциал,
представляет собой полный дифференциал, 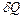 и
и 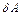 не являются полными дифференциалами.
не являются полными дифференциалами.
Теплоемкостью тела называют величину, равную количеству теплоты 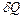 , которую нужно сообщить телу (отнять от тела), чтобы изменит его температуру
, которую нужно сообщить телу (отнять от тела), чтобы изменит его температуру 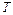 на 1 K:
на 1 K:
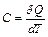 .
.
Теплоемкость единицы массы вещества 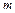 называется удельной теплоемкостью:
называется удельной теплоемкостью: 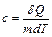 . Ее размерность – [Дж/(кг×К)].
. Ее размерность – [Дж/(кг×К)].
Теплоемкость одного моля вещества 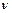 называется молярной теплоемкостью:
называется молярной теплоемкостью: 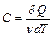 .Ее размерность – [Дж/(моль×К)].
.Ее размерность – [Дж/(моль×К)].
Удельная и молярная теплоемкости связаны соотношением:
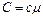 ,
,
где 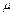 – молярная масса вещества.
– молярная масса вещества.
Найдем теплоемкости газа при различных условиях:
1. Изохорный процесс для одного моля вещества (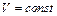 ). В этом случае работа, совершаемая газом при нагревании, равна:
). В этом случае работа, совершаемая газом при нагревании, равна:
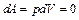
и первый закон термодинамики запишется в виде:
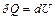 ,
,
т.е. все количество теплоты, переданное газу, идет на увеличение его внутренней энергии. Тогда получаем для молярной теплоемкости при 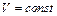 :
:
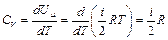 . (2.3)
. (2.3)
2. Изобарный процесс для одного моля вещества (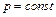 ). В данном случае количество теплоты, переданное газу, идет на увеличение его внутренней энергии и на совершение им работы против внешних сил:
). В данном случае количество теплоты, переданное газу, идет на увеличение его внутренней энергии и на совершение им работы против внешних сил:
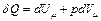 .
.
Из уравнения Менделеева–Клайперона следует, что 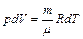 и для одного моля идеального газа имеем
и для одного моля идеального газа имеем 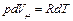 ,
,
тогда:
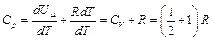 . (2.4)
. (2.4)
Соотношение 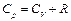 называется уравнением Майера.
называется уравнением Майера.
 2015-09-06
2015-09-06 245
245








