Для увеличения температуры тела к нему необходимо подвести некоторое количество тепла. Экспериментально установлено, что для большинства тел изменение их температуры пропорционально величине подводимого тепла. Коэффициент пропорциональности называется теплоёмкостью тела:
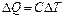 , (9.1)
, (9.1)
где 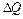 – подведенное тепло,
– подведенное тепло, 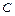 – теплоемкость,
– теплоемкость, 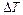 – изменение температуры.
– изменение температуры.
Если сравнить два тела, изготовленные из одного материала, массы которых отличаются в два раза, то очевидно, что для нагрева более тяжелого тела потребуется в два раза больше энергии, чем для нагрева более легкого тела до той же температуры. Поэтому, наряду с коэффициентом теплоёмкости, рассматривается коэффициент удельной теплоёмкости, который характеризует вещество, из которого изготовлено тело, и равен теплоёмкости единицы массы этого вещества:
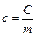 , (9.2)
, (9.2)
где 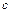 – удельная теплоёмкость вещества,
– удельная теплоёмкость вещества, 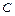 – теплоёмкость тела, изготовленного из этого вещества,
– теплоёмкость тела, изготовленного из этого вещества, 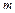 – масса тела. Заметим, что теплоёмкость является величиной аддитивной. То есть, если совместно нагревать два тела, теплоёмкости которых равны
– масса тела. Заметим, что теплоёмкость является величиной аддитивной. То есть, если совместно нагревать два тела, теплоёмкости которых равны 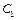 и
и 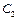 , то теплоёмкость тела, сложенного из этих двух, будет равна:
, то теплоёмкость тела, сложенного из этих двух, будет равна:  .
.
Из теории идеального газа известно, что средняя кинетическая энергия одноатомных молекул: 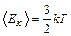 , где
, где 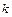 - постоянная Больцмана. Среднее значение полной энергии частицы при колебательном движении в кристаллической решетке:
- постоянная Больцмана. Среднее значение полной энергии частицы при колебательном движении в кристаллической решетке: 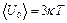 . Полную внутреннюю энергию одного моля вещества твёрдого тела получим, умножив среднюю энергию одной частицы на число независимо колеблющихся частиц, содержащихся в одном моле, т. е. на число Авогадро:
. Полную внутреннюю энергию одного моля вещества твёрдого тела получим, умножив среднюю энергию одной частицы на число независимо колеблющихся частиц, содержащихся в одном моле, т. е. на число Авогадро:
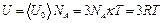 , (9.3)
, (9.3)
где 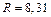 Дж/(моль×К) - универсальная газовая постоянная.
Дж/(моль×К) - универсальная газовая постоянная.
Для твёрдых тел, вследствие их малого коэффициента теплового расширения, теплоёмкости при постоянном давлении 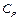 и постоянном объёме
и постоянном объёме 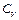 практически не различаются. Поэтому с учетом формулы (10.3), молярная теплоёмкость твёрдого тела будет определяться как:
практически не различаются. Поэтому с учетом формулы (10.3), молярная теплоёмкость твёрдого тела будет определяться как:
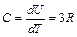 . (9.4)
. (9.4)
Молярная теплоёмкость может быть представлена как произведение молярной массы 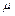 на величину удельной теплоёмкости
на величину удельной теплоёмкости 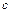 :
: 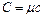 . Подставляя численное значение универсальной газовой постоянной, получим:
. Подставляя численное значение универсальной газовой постоянной, получим:  Дж/(моль×К). Равенство (9.4), называемое законом Дюлонга и Пти, выполняется с довольно хорошим приближением для многих веществ при комнатной температуре и позволяет рассчитать по известным значениям удельной теплоёмкости молярные массы простых кристаллических твёрдых тел.
Дж/(моль×К). Равенство (9.4), называемое законом Дюлонга и Пти, выполняется с довольно хорошим приближением для многих веществ при комнатной температуре и позволяет рассчитать по известным значениям удельной теплоёмкости молярные массы простых кристаллических твёрдых тел.
Со снижением температуры теплоёмкость твёрдых тел уменьшается, приближаясь к нулю при 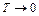 . Вблизи абсолютного нуля молярная теплоёмкость всех тел пропорциональна
. Вблизи абсолютного нуля молярная теплоёмкость всех тел пропорциональна 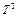 , и только при достаточно высокой, характерной для каждого вещества, температуре начинает выполняться равенство (9.4). Эти особенности теплоёмкостей твёрдых тел при низких температурах можно объяснить с помощью квантовой теории Энштейна и Дебая.
, и только при достаточно высокой, характерной для каждого вещества, температуре начинает выполняться равенство (9.4). Эти особенности теплоёмкостей твёрдых тел при низких температурах можно объяснить с помощью квантовой теории Энштейна и Дебая.
Для экспериментального определения теплоёмкости исследуемое тело помещается в калориметр. Если температуру калориметра с исследуемым образцом очень медленно увеличивать от начальной 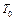 (комнатной температуры) до некоторой температуры
(комнатной температуры) до некоторой температуры 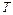 , причем
, причем 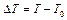 , то энергия электрического тока
, то энергия электрического тока 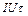 будет расходоваться на нагревание образца
будет расходоваться на нагревание образца 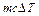 и калориметра
и калориметра 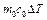 :
:
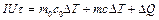 , (9.5)
, (9.5)
где 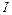 и
и 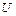 - сила тока и напряжение нагревателя;
- сила тока и напряжение нагревателя; 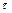 - время нагревания;
- время нагревания; 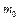 и
и 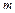 - массы калориметра и исследуемого образца;
- массы калориметра и исследуемого образца; 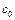 и
и 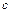 - удельные теплоёмкости калориметра и исследуемого образца;
- удельные теплоёмкости калориметра и исследуемого образца; 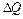 - потери тепла в теплоизоляцию калориметра и в окружающее пространство.
- потери тепла в теплоизоляцию калориметра и в окружающее пространство.
Для исключения из уравнения (9.5) количества теплоты, израсходованной на нагрев калориметра и потери теплоты в окружающее пространство, необходимо при той же мощности нагревателя нагреть пустой калориметр (без образца) от начальной температуры 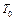 на ту же разность температур
на ту же разность температур 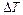 . Потери тепла в обоих случаях будут практически одинаковыми и малыми, если температура защитного кожуха в обоих случаях постоянна и равна комнатной:
. Потери тепла в обоих случаях будут практически одинаковыми и малыми, если температура защитного кожуха в обоих случаях постоянна и равна комнатной:
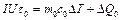 . (9.6)
. (9.6)
Из уравнений (9.5) и (9.6) следует:
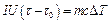 . (9.7)
. (9.7)
Уравнение (9.7) может быть использовано для экспериментального определения удельной теплоёмкости исследуемого материала. Изменяя температуру калориметра, необходимо построить график зависимости времени нагрева от изменения температуры исследуемого образца 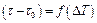 , по угловому коэффициенту которого
, по угловому коэффициенту которого 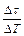 равного
равного 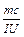 можно определить удельную теплоёмкость образца
можно определить удельную теплоёмкость образца 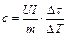 .
.
 2015-09-06
2015-09-06 226
226








