Біном Ньютона

3.1. Обчислити: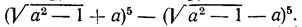

3.2. Знайти коефіцієнт при х ⁵ у многочлені

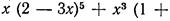
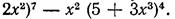
3.3. Знайдіть раціональні доданки в розкладі біному:

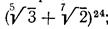
3.4. Знайдіть раціональні доданки в розкладі біному:

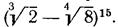
3.5. Знайдіть раціональні доданки в розкладі біному:

.

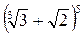3.6. У біноміальному розкладі 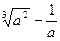знайдіть доданок, який не містить а.

3.7. Сума коефіцієнтів першого, другого й третього членів біноміального розкладу (а + b) ⁿ дорівнює 46. Знайдіть n.

3.8. Коефіцієнти другого, третього й четвертого членів біноміального розкладу 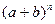утворюють арифметичну прогресію. Визначити n.

3.9. Коефіцієнти четвертого й шостого членів біноміального розкладу 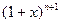рівні між собою. Визначити п.

3.10. Довести, що сума коефіцієнтів у біноміальному розкладі(З х – 2 у) ⁿ при будь-якому п дорівнює 1.

3.11. У розкладі бінома 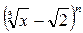знайти член, що містить х ⁴, якщо коефіцієнт третього члена дорівнює 90.

3.12. Знайти показник степеня бінома 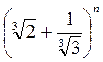, якщо відношення сьомого члена його розкладу від початку до сьомого члена від кінця дорівнює 0,1(6).

3.13. У розкладі бінома 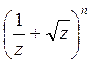коефіцієнт четвертого члена відноситься до коефіцієнта шостого члена, як 5:18. Знайти в цьому розкладі доданок, що не залежить від z.

3.14. Знайти х, якщо п'ятий член розкладу бінома 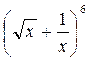дорівнює .

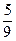3.15. У розкладі бінома 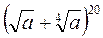знайти доданок, що містить а ⁷.

3.16. Коефіцієнти п'ятого, шостого і сьомого членів розкладу бінома (1 + х)^п утворюють арифметичну прогресію. Знайти п.

3.17. При якому значенні х третій доданок розкладу бінома 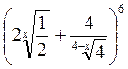дорівнює 240?

3.18. Який доданок розкладу бінома 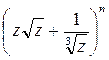містить z ⁵ , якщо сума біноміальних коефіцієнтів цього розкладу дорівнює 128?

3.19. Знайти х, у і z, якщо відомо, що другий, третій і четвертий члени розкладу (х + у) ^z відповідно дорівнюють 240, 720 і 1080.

3.20. Знайти найбільший член розкладу бінома .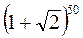

3.21. Коефіцієнти четвертого і шостого членів розкладу бінома (1+ х) ^{n +1}рівні між собою. Знайти п.

3.22. Знайти показник бінома 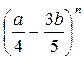, якщо в його розкладі сума всіх показників степенів числа b дорівнює 36.

3.23. Сума біномінальних коефіцієнтів розкладу (1+ х) ⁿ +(1+ x) ^{n +1}дорівнює 1536. Знайти коефіцієнт при х ⁶.